maturzysta: Czy ten przykład można rozwiązać sposobem jaki został zastosowany w przykładach: https://matematykaszkolna.pl/strona/3937.html https://matematykaszkolna.pl/strona/3938.html Taki sposób rozwiązywania jest krótszy i dlatego stwarza mniej okazji do popełniania błędów. A wtedy w przykładzie:

3x+7
	=|8−4x|
5x−11

jest tak że:

3x+7
	=8−4x
5x−11

lub

	3x+7
−		=8−4x
	5x−11

Jakub, w jednym z komentarzy pod resztą przykładów napisałeś, że mnożenie na krzyż jest szybsze, ale nie można go stosować w przypadku nierówności, dlatego stosujesz sposób jak np. tutaj: https://matematykaszkolna.pl/strona/3978.html. A powyższy sposób? Można go stosować w ww. przypadku oraz w przypadku nierówności?

Jakub: Nie możesz zastosować do równania

3x+7
	= |8−4x|
5x−11

sposobów ze stron https://matematykaszkolna.pl/strona/3937.html https://matematykaszkolna.pl/strona/3938.html W tamtych równaniach masz po prawej stronie liczbę dodatnią. W równaniu

3x+7
	= |8−4x|
5x−11

masz natomiast wartość bezwzględną. Jak rozwiążesz dwa równania

	3x+7		3x+7
−		= 8−4x i		= 8−4x
	5x−11		5x−11

	3x+7
to może się zdarzyć, że otrzymasz rozwiązane, które podstawione pod		da
	5x−11

	3x+7
liczbę ujemną, a przecież		ma się równać wartości bezwzględnej. Tego jednak nie
	5x−11

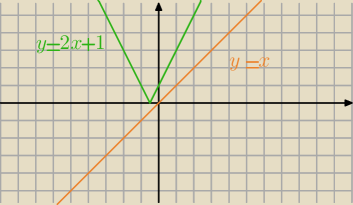
zauważysz, bo opuściłeś wartość bezwzględną. Zobacz na innym dużo prostszym przykładzie x = |2x+1| opuszczam wartość bezwzględną tak jak ty i mam −x = 2x + 1 lub x = 2x+1 Liczę i mam dwa rozwiązania

	1
x = −		lub x = −1
	3

Jednak jak podstawisz je do x = |2x+1|, to się przekonasz, że to nie są prawidłowe rozwiązania. Równanie x = |2x+1| jest sprzeczne. Nie ma rozwiązań. Zresztą to widać na rysunku. Podsumowując, jak masz wartość bezwzględna równa się wyrażenie, a nie liczba, to nie możesz to liczyć rozpatrując dwa przypadki jak dla liczby. Trzeba to robić za pomocą przedziałów. Tak jak w przykładzie na stronie 1109