ukulele: A co z wzorem na odległość między dwoma prostymi równoległymi? Nie widzę tutaj nigdzie tego wzoru...

Jakub: Tutaj 1254 masz przykład, jak można policzyć odległość między dwoma prostymi równoległymi. Oczywiście jest na to wzór. Ja korzystam jednak z minimalnej ilości wzorów i jeśli się da liczę wszystko "na piechotę".

soulee: Koło w ukł. wspołrzednych − matura podstawowa. Nawet dzis w wyborczej dali zadanko z koła w układzie.

soulee: a, nie sorry, okrąg

Jakub: Na podstawie jest tylko równanie okręgu: (x−a)²+(y−b)² = r² Na rozszerzeniu dochodzi jeszcze nierówność opisująca koło: (x−a)²+(y−b)² ≤ r²

Alastor: pomocy mam zadanko Punkt A' = (−a + 2,4) jest obrazem punktu A = (−5,b , 3) w symetrii względem osi Ox. Wyznacz a i b

Jakub: Zadania umieszczaj na forum zadankowym.

Kama: Jak się oblicza odległość punktu od prostej?

Jakub: Zobacz w spisie treści na poprzedniej stronie.

Gustlik: Jakubie − jeżeli możesz, podaj wzór na wyznacznik wektorów oraz na pole trójkąta liczone z tego wyznacznika: u^→=[u_x, u_y] v^→=[v_x, v_y] Wyznacznik wektorów: d(u^→, v^→)= |u_x u_y| = u_x*v_y−u_y*v_x |v_x v_y| (na krzyż pierwsza przekątna minus druga przekątna) Pole trójkąta: Z dwóch boków robimy wektory w ten sposób, aby miały wspólny początek, np. AB^→ i AC^→ i liczymy ich współrzędne AB^→=[x_B−x_A, y_B−y_A], AC^→=[x_C−x_A, y_C−y_A]: Wzór na pole:

	1
P=		|d(AB→, AC→)|
	2

gdzie d(AB^→, AC^→) − wyznacznik wektorów AB^→ i AC^→ Pole równoległoboku: Z dwóch sąsiednich boków robimy wektory w ten sposób, aby miały wspólny początek, np. AB^→ i AD^→ i liczymy ich współrzędne AB^→=[x_B−x_A, y_B−y_A], AD^→=[x_D−x_A, y_D−y_A]: Wzór na pole: P=|d(AB^→, AD^→)| gdzie d(AB^→, AD^→) − wyznacznik wektorów AB^→ i AD^→

Gustlik: Za pomocą wyznacznika wektorów można wyznaczyć pole dowolnego czworokąta i w ogóle dowolnego wielokata, jeżeli dane są współrzędne jego wierzchołków. Robimy to w następujący sposób: z jednego z wierzchołków, np. A wyprowadzamy wektory do wszystkich pozostałych wierzchołków tego wielokąta i liczymy współrzędne tych wektorów. Dwa z tych wektorów będą bokami wielokąta, pozostałe będą przekatnymi. W ten sposób podzielimy wielokąt na trójkąty. Pola tych trókątów wyznaczymy ze wzoru wyznacznikowego opisanego w powyższym poście, np.

	1
P1=		|d(AB→, AC→)|
	2

	1
P2=		|d(AC→, AD→)|
	2

	1
P3=		|d(AD→, AE→)|
	2

itd... aż do końca. Następnie sumujemy tak obliczone pola trójkątów i mamy pole całego wielokąta.

ceaser I: trochę mało zadań z wektorami do rozwiązania

nnnnn: hm, moze ma ktos caly sprawdzian, z tego dzialu . i korzysta z ksiazki k. pazdro

Gustlik: Moje "poprawki" − tak powinien wyglądać program nauczania z tego działu: podstawy rozszerzenia studia równanie kierunkowe prostej równanie ogólne prostej proste równoległe i prostopadłe kąt nachylenia prostej do osi Ox punkty których współrzędne spełniają nierówności wzór na kąt miedzy prostymi prosta przechodząca przez dwa punkty odległość dwóch punktów od siebie środek odcinka odległość punktu od prostej o danym równaniu okrąg w układzie współrzędnych koło w układzie współrzędnych rysowanie wektorów współrzędne wektorów długość wektora kierunek i zwrot wektora. Wektory równe. Wektory przeciwne. dodawanie wektorów odejmowanie wektorów mnożenie wektora przez liczbę iloczyn skalarny wektorów kąt między wektorami wektor prostopadły do prostej wektor równoległy do prostej

piotrek: Podstawą ostrosłupa jest trójkąt prostokątny o przyprostokątnych 16cm i 12cm. Oblicz objętość tego ostrosłupa, wiedząc, że każda krawędź boczna tworzy z płaszczyzną podstawy kąt 60° V=1/3*Pp*H Pp = (16*12)/2 = 96 nie wiem tylko jak wyznaczyć tę cholerną wysokość. zrobilbym tak: opisuję okrąg na podstawie. spodek wysokości leży na środku okręgu, z kolei srodek okręgu lezy w polowie przeciwprostokątnej naszego trójkąta. tg60 = H/10 => H = 10*√3 pozdrawiam, będę wdzieczny za wszelką pomoc

piotrek: ups, w zlym miejscu, przepraszam

nina: naszkicuj wykres funkcji f(x)= x+3 dla x (−∞ ,−2) , f(x)= 1 dla x (−2,−1) , f(x)=x kwadrat dla x (−1,∞) ; podaj jej miejsce zerowe ; dla jakich argumentów funkcja przyjmuje wartości dodatnie a dla jakich ujemne ; podaj przedziały w których funkcja jest rosnąca , malejąca , stała ;naszkicuj wykres funkcji g(x)= −f(x)

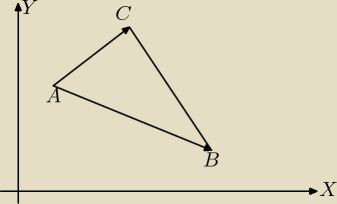
Gustlik: Dodam rysunek do "wektorowego" wzoru na pole trójkąta:

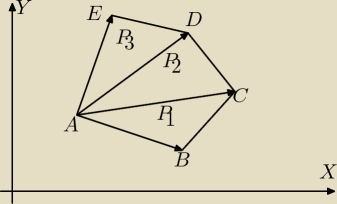
Gustlik: Dodam rysunek do "wektorowego" wzoru na pole wielokąta − dla przykladu zobrazuję na pięciokącie. Liczymy wyznacznikami wektorów pola trójkątów P₁, P₂, P₃ itd..., potem sumujemy te pola i mamy pole wielokąta. Dodam, że tą metodą można obliczać pola figur, gdy figura narysowana jest w podręczniku "po kratkach", nawet gdy nie ma układu współrzędnych. Wystarczy do potrzebnych wektorów dorysować składową poziomą (traktujemy ją jak współrzedną x wektora) oraz pionową (traktujemy jak współrzędną y), z kratek odczytujemy wartosci tych współrzędnych, a potem liczymy wyznaczniki i z nich pola. Należy pamiętać, że zwrot składowej poziomej prawo oznacza dodatnia współrzędną x wektora a w lewo − x ujemne. Tak samo ze współrzędną y − składowa pionowa w górę − y dodatnie, a w dół − y ujemne.

lol: αβγδπΔΩ∞≤≥∊⊂∫→⇒⇔⇔⇔∑≈≠≠≠≠♦♥

Kate: Dlaczego nie ma tu zadań do tematów z wektorów

Mateusz: dzien dobry, mam pytanie czy pan jest nauczycielem od matematyki czy pan po prostu umie matme?

Jakub: Umiem matmę i kiedyś udzielałem dużo korepetycji z matematyki. Takim nauczycielem w szkole nie jestem.

Mateusz: Aha rozumiem

Gustlik: Jakubie, ja bym dodał tutaj oraz do funkcji liniowej jeszcze jedną rzecz: że wektor o danych współrzędnych zawsze wyznacza kierunek prostej, a więc z wektora można łatwo obliczyć wspołczynnik kierunkowy prostej, na której dany wektor leży, oraz każdej prostej równoległej do niego. Jeżeli w^→=[w_x, w_y] i w_x≠0, to współczynnik kierunkowy a=U{w_y}{w{x}. Gdy w_x=0, to wektor ma kierunek rownoległy do osi OY, czyli "pionowy", mamy wtedy prostą "pionową" o równaniu x=c. Wynika to ze wzorów:

	yB−yA
AB→=[xB−xA, yB−yA] oraz a=		.
	xB−xA

Dlatego z wektorów najłatwiej wyznaczyć współczynnik kierunkowy i ja tego uczę na poziomie PODSTAWOWYM. Można w ten sposób łatwo wyznaczyć współczynnik kierunkowy prostej przechodzącej przez dwa punkty, a z tego współczynnika w zależności od potrzeb np. równanie całej prostej przechodzącej przez dwa punkty, równanie symetralnej odcinka, wysokości trójkąta albo równanie innej prostej równoległej lub prostopadłej do danej przechodzącej punkt o danych współrzędnych. Można też łatwo zbadać prostopadłość lub równoległość wektorów nie znając własności iloczynu skalarnego czy wektorowego, które niestety zostały wycofane z podstawy programowej nawet na rozszerzeniu, wystarczy z wektorów obliczyc wspołczynniki kierunkowe i jeżeli wyjdą równe − to

	1
mamy wektory i proste równoległe, jeżeli a2=−		to mamy wektory i proste prostopadłe,
	a1

a jeżeli nie wyjdzie żaden z tych warunków, to proste przecinają się pod kątem innym niż prosty. Można w ten sposób łatwo zbadać, czy trójkąt o podanych współrzędnych wierzchołków jest prostokątny − obliczyć współrzędne wektorów tworzących boki trójkąta i z tych wektorów

	1
obliczyć współczynniki kierunkowe. Jeżeli dwa z nich spełniają zależność a2=−		, to
	a1

trójkat jest prostokątny. Szybszy i łatwiejszy sposób niż wyliczanie długości boków i sprawdzanie Pitagorasem.

Gustlik: Poprawiam chochlika:

	wy
Jeżeli w→=[wx, wy] i wx≠0, to współczynnik kierunkowy a=		.
	wx

Jakub: Wszystko prawda. Użycie wektorów w wielu zadaniach upraszcza obliczenia. Niestety wektory są dopiero na poziomie rozszerzonym, a i to w okrojonym zakresie. Raczej wiele osób na poziomie podstawowym niechętnie by do nich podeszło, bo 1. nie ma tego na podstawie, 2. nie mieli tego w szkole.

MONIKAAAA: zad1 Wyznacz równanie prostej k przechodzącej przez punkt P(−14) i nachylonej do Osi OX pod katem 45stopni. zad2. Napisz równanie prostej m przechodzącej przez punkt P(5,−2) i równoległej do 4x+y−6=0 proszę o rozwiązanie

Gustlik: Jakubie ja wiem, ze wektory sa na rozszerzeniu, choć nie kumam dlaczego, bo są banalnie proste i uczniowie z podstaw, nawet słabi, je rozumieją. Wiem coś na ten temat, bo u mnie wektory to PODSTAWA geometrii analitycznej i pokazuję je każdemu. Co jest trudnego w odjęciu współrzędnych dwóch punktów? To proste jak konstrukcja młotka. Wystarczy znać dodawanie i odejmowanie, 6−klasista by to zrobił. Użycie wektorów radykalnie upraszcza zadania z geometrii analitycznej, poza tym raz obliczone współrzędne wektorów przydają się nieraz do obliczenia kilku wielkości w zadaniu, np. do współczynnika kierunkowego i równania prostej, do długości odcinków, do pola trójkąta i pól innych figur, bez wektorów każdą taką wielkość trzeba liczyć od początku i dużo dłużej. A dużo dłużej = więcej czasu, mniej punktów na maturze i większe ryzyko pomyłki.

Gosc: Oby tak dalej, prosimy o więcej materiałów ze studiów

Błażej: Dany jest trójkąt o wierzchołkach A(2,1) B(1,5) C(−7,3) oblicz jego obwód i pole. Poprosiłbym o podanie wyników + rozwiązanie i wytłumaczenie Z góry dziękuję

kocur: geometria analityczna nie działa

Jakub: Co znaczy nie działa?

Marysia: Bardzo prosze pomógłby mi ktoś ? Mam zrobic zadanie a nwm całkowicie jak : Wyprowadz wzór symetri wzgledem dowolnej prostej y=ax+b Sy=ax+b (x,y)

mary(sia): ciekawie o geometrii analitycznej jest tu http://urbmat.pl/kategoria.php?id=4

francesca: Oblicz kąt pomiędzy funkcjami (gradientem) arctg(x/y)=(e^x)−1 i y=x² Proszę o szybką odpowiedź

schabs: Potrzebuję pomocy pilnej z: x²+y²−4y+3≤0