Patryk: Dlaczego wyznaczając dziedzinę przyrównał pan oprócz mianowników obu ułamków takze licznik tego drugiego ?

Knazin z Bazin: Też tego nie kminie!

Jakub: Mam dzielenie dwóch wyrażeń wymiernych. Mianowniki nie mogą być równe zero, wiadomo dlaczego. Kreska ułamkowa zastępuje znak dzielenia, wiec aby nie było dzielenia przez zero, trzeba wyrzucić z dziedziny liczby, które dają w mianowniku zero. Podobnie przy dzieleniu dwóch wyrażeń wymiernych, to drugie wyrażenie nie może być równe zero, abym nie dzielił przez zero. Dlatego się zastanawiam, kiedy to drugie wyrażenie jest równe zero. Jest równe zero, gdy licznik drugiego wyrażenia jest równe zero.

Gustlik: Albo inaczej − ja to tłumaczę tak: dzielenie ułamków zastępujemy mnożeniem pierwszego ułamka przez odwrotność drugiego, tak jak na ułamkach "liczbowych", czyli

	a		c		a		d
		:		=		*		. Założeniu podlegają więc zarówno oba mianowniki dzielonych
	b		d		b		c

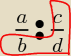
ułamków, czyli wyrażenia b i d, bo nie mozna dzielić przez zero oraz licznik drugiego ułamka − wyrażenie c, bo po zamianie na mnożenie przez odwrotność stanie się on mianownikiem i będziemy przez niego dzielić, a dzielenie przez zero jest nieokreślone. Na rysunku schemat wyznaczania dziedziny przy dzieleniu wyrażen wymiernych − rysujemy takiego "buta" − (czerwona linia) − wyrazenia w "bucie" muszą być różne od 0.

Jakub: Ładny "wizualny" sposób na zapamiętanie tego, co nie może być równe zero.

Lidka: Dziękuję za wytłumaczenie Gustlik. Moją pasją jest matematyka. Od mojej matury minęło 20 lat. Lubię sobie przypominać materiał ze szkoły średniej. Jakubie dziękuję za stronę.

Madlen: Chciałabym, żeby matematyka byłam moją pasja... Niestety dla mnie ona jest wysłannikiem diabla, chyba jestem zbyt głupia aby to pojąć :<

Jakub: Przynajmniej przekonujesz się o swoich słabych i mocnych stronach. To też zaleta znać swoje ograniczenia.