endrju: Warto byłoby dodać obliczanie granic korzystając z definicji liczby e, co bardzo często się stosuje (przynajmniej na studiach).

aa: w liceum na rozszerzonej matematyce także się stosuje

zordon:

	2x(x−5)2
jak zrobić lim x→3		omg zawaliłem porawe:(
	2x

Jakub: Po prostu podstaw za x liczbę 3. Wyjdzie ci sensowny wynik.

niekumaty: mam takie banalne pytanie: ) granica ciagu→∞ pierwiastka z n = ∞?

Jakub: Tak niekumaty

Michał ;): mam pytanie...głupie może..jak obliczyć taki przykład (znam wynik ale nie wiem jak do niego dojsc) :

	√2n + 3
lim x→∞
	3n−2

z góry dziekuję za pomoc

j: stopien licznika (potega przy n) jest mniejszy od stopnia mianownika, wiec caly ciag zmierza do 0

sandra: ⁿ√2*3ⁿ+4*7ⁿ

sandra: Ten powyższy ciag moge poprostu rozwiac tak: lim ⁿ√6ⁿ+28ⁿ=lim 6+28=lim 34. czy to jest zle rozwiązanie?

Jakub: Twój sposób jest niepoprawny. Nie wolno tak pierwiastkować sumy. Zobacz: √9+16 = 3+4 = 7 (według ciebie). √9+16 = √25 = 5 (poprawnie). Twoim sposobem można pierwiastkować iloczyn. √9*16 = 3*4 = 12 √9*16 = √144 = 12 Twoje zadanie robi się z twierdzenia o trzech ciągach ⁿ√4*7ⁿ ≤ ⁿ√2*3ⁿ + 4*7ⁿ ≤ ⁿ√2*7ⁿ + 4*7ⁿ 7ⁿ√4 ≤ ⁿ√2*3ⁿ + 4*7ⁿ ≤ ⁿ√6*7ⁿ 7ⁿ√4 ≤ ⁿ√2*3ⁿ + 4*7ⁿ ≤ 7ⁿ√6 Lewy ciąg 7ⁿ√4 dąży do 7, bo ⁿ√4 dąży do 1. Prawy ciąg 7ⁿ√6 dąży do 7, bo ⁿ√6 dąży do 1. Środkowy ciąg musi też dążyć do 7.

inżynier...: dlaczego środkowy ciąg dąży do 7?

Jakub: Wynika to z twierdzenia o trzech ciągach. Jak dwa ograniczające po obu stronach ciągi dążą do 7, to środkowy też musi dążyć do 7.

jakie 0?: a mógłbys pokazac na jakiś przykładach jak granica z ułamka w którym mianownik jest zerem jest np. rowny 1? co jest niby wbrew logice ze nie wolno dzielic przez zero a tutaj jakies takie przypadki. i Jakub moglbys napisac o co chodzi z tym zerem>//

Zuzka: a ja mam może dziwne pytanie, ale zaryzykuję, a mianowicie, skąd mam wiedzieć czy ciąg dąży do nieskonczoności czy zera, jeżeli nie jest podane czy a jest większe od zera czy mniejsze. Bo mając a³ w przypadku a jako ułamka dążymy do zera, a w przypadku a liczby całkowitej dążymy do nieskonczonośći... nie rozumeim tego kompletnie. Mam nadzieję, że wyraziłam się dosyć jasno pozdrawiam!

Jakub: Jak nic nie wiem o "a", to nie policzę jego granicy. W zadaniach jest jednak zazwyczaj liczba w podstawie. Wystarczy zobaczyć, jaki warunek spełnia. a > 1 granica = +∞ a = 1 granica = 1 −1 < a < 1 granica = 0 a = −1 granicy nie ma, bo (−1)ⁿ = (−1, 1, −1, 1, ...) a < −1 granicy nie ma, bo np. (−2)ⁿ = (−2, 4, −8, 16, −32, ...) Rozpisałem dokładniej wzory na granicę potęg z poprzedniej strony.

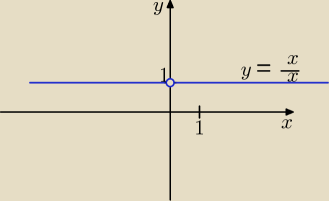
ebi: jaka jest granica ciągu l i m ^x_x ^x→∞ funkcja jest nieciągła w punkcie A(0;1) bo podobno 1. ale ^∞_∞ to symbol nieoznaczony, jeżeli szukając granicy podstawiamy l i m f(x) = f(x₀) ^x→x₀ tu x₀ = ∞ , więc wychodzi .

manius: Witam, mam problem z granicą lim x→4 ^{x2 − 6x +8}_{x − 4} wydaje mi się, że nie wystarczy podstawić za x 4, zbyt prosto by było, chyba że się mylę. Proszę o jakieś wskazówki...

manius: zadanie wyżej przeniosłem na forum zadankowe, pozdrawiam

foka: Pomóżcie obliczyć granice ciągu− proszę

3n+2
5 √n2−1−3

m: 4ⁿ⁺¹−5ⁿ⁺² /5ⁿ−4ⁿ jak to obliczyc?

m: √3⁵ +1 / √n⁵+1 +1 n⁵+1 jest pod jednym pierwiastkiem

m: pomylka √n⁵ +1 / √n⁵ +1+1

3mps: wracajac do przykladu sandry limⁿ√2*3ⁿ + 4*7ⁿ w rozwiazaniu z wykorzystaniem twierdzenia o trzech ciagach rozpisałes to w nastepojacy sposob: ⁿ√4*7ⁿ ≤ ⁿ√2*3ⁿ + 4*7ⁿ ≤ ⁿ√2*7ⁿ + 4*7ⁿ dlaczego w taki sposob wykonałes ten rozkład chodzi mi o lewy i prawy ciag. rozkladu dokonujemy zawsze ze wzgledu na wieksza liczbe pod pierwiastkiem czy dowolnie? choc w tedy wyszła by dlatego przykładu granica 3 nie rozumiem zbytnio tego rozkładu czy do tego przykładu mozna podac jakis inny rozkład? jesli tak to jaki?

Jakub: To nie jest rozkład. Zamiast 2*3ⁿ + 4*7ⁿ napisałem po lewej stronie 4*7ⁿ, ponieważ musiałem napisać coś mniejszego. Potęga 4*7ⁿ na pewno jest mniejsza od 2*3ⁿ + 4*7ⁿ. Podobnie po prawej stronie musiałem napisać coś większego. W ten sposób środkowy ciąg został ograniczony z obu stron przez dwa ciągi, których granica jest równa. To właśnie było najtrudniejsze, aby po lewej i po prawej stronie dobrać ciągi, których granica jest równa. W ten sposób mam pewność, że środkowy ciąg zbiega do tej samej granicy, co ciągi po obu stronach.

Szach: Może głupie pytanie, ale co oznacza to n→∞ pod lim, skoro np. dla (1/2)ⁿ granicą będzie 0? Czy po prostu zawsze pisze się to wyrażenie "n→∞", czy to jednak coś oznacza?

hooltay:

	1
lim n→∞(n+4) do potęgi
	n+4

jak to obliczyć?

aga: granice x dąży do 1 z lewej albo z prawej stron O co chodzi jak jest granica lim x→1− albo lim x→0+ albo lim x→π/2− wogóle tego nie rumiem

Kuba: pierwiasten "n−tego"stopnia z ³ⁿ⁺⁴ⁿ_5ⁿ+10ⁿ brzydko wychodził zapis przy pomocy komendy na pierwiastek wiec zapisalem jak zapisalem Proszę o pomoc niewiem co zrobić z tym mianownikiem, wiem ze musze wykożystactwierdzenie o 3 ciągach ale ten mianownik

Kuba: chodzi oczymiscie o granice z powyzszego wyrazenia

gabi266: Zbadaj istnienie granicy ciągu o wyrazie ogólnym ∑(1/k²) i ta suma jest od k=1 do n jakie etapy musze zrobic aby zbadac czy isnieje granica?

confused:

	x+5
lim (		) do 3x
	x

x→∞ Wyrażenie oznaczone mam podane z zajęć 1^∞ − mógłby ktoś wytłumaczyć skąd wzięła się 1 ?

confused:

	x+5
lim (		) do 3x
	x

x→∞ Wyrażenie oznaczone mam podane z zajęć 1^∞ − mógłby ktoś wytłumaczyć skąd wzięła się 1 ?

Jakub:

x+5		x		5		5		5
	=		+		= 1 +		Dla x→∞ mam		→0
x		x		x		x		x

dominik04u: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=3672 treść zadania jest na tej stronie. Przepraszam, że tak je tu podaję

Magda: mam problem z rozwiązaniem granicy: lim ^1+2+3+...+n_{√4n⁴+3n+1} n→∞

Kuba: Jakub, chyba masz błąd w drugim przykładzie gdzie 2/n −> 1 (powinno być 2/n −>0).

Jakub: Dzięki, już poprawiłem Kuba