Gustlik: Krótko mówiąc: wykres funkcji parzystej jest osiowo symetryczny względem osi OY (np. parabola y=x²), a wykres funkcji nieparzystej jest środkowo symetryczny wzgędem początku układu współrzędnych, czyli punktu przecięcia obu osi (0, 0) − obracając ten wykres względem tego punktu o kąt 180 stopni otrzymamy ten sam wykres (np. krzywa y=x³). Wykres funkcji, która nie jest ani parzysta, ani nieparzysta, nie jest symetryczny ani względem osi OY ani względem punktu (0,0), ale może mieć oś lub środek symetrii w innym miejscu.

Osioł : f(−x) = −f(x) <− nie rozumiem skąd się to wzięło. To co zapisane jest powyżej jak najbardziej.

Jakub: Zobacz na rysunek funkcji nieparzystej na poprzedniej stronie. f(−5) = −4 f(5) = 4 czyli f(−5) = −f(5). Tak jest dla wszystkich x, co można zapisać równaniem f(−x) = −f(x). Takie funkcje nazywamy funkcjami nieparzystymi.

Ola: hmm a np taka funkcja jest pazysta czy nieparzysta? f(x) = √14−x²

lukasz: parzysta, bo liczysz f(−x)=√14−(−x)² czyli wychodzi z tego √14−x² co jest równe f(x) czyli z definicji f(−x)=f(x)

ysiulec: Warto dodać, że to, że funkcja nie jest parzysta nie oznacza jednocześnie, że jest nieparzysta. Przydałoby się kilka zadań w jaki sposób sprawdzić czy jest parzysta, czy też nie.Jeżeli dobrze pamiętam, najpierw należy sprawdzić dziedzinę funkcji, później zgodnie z definicją: f(x) = f(−x) tam wszędzie, gdzie jest x (słonie w karawce) musimy dać minus ALE jeśli x jest w potędze, to w nawiasie. Musimy pamiętać, że wtedy najpierw wykonujemy potęgowanie. Myślę, że autor wie o co chodzi. BTW brakuje mi również zadań z parametrem m.

Kamil: to jest materiał ze studiów? ja mam to na matmie w pierwszej klasie i nie jestem w klasie rozszerzonej, masakra

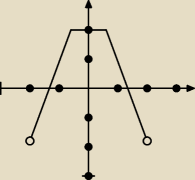
Kapucha: rozumiem że to jest parzyste...?bo jeśli tak to w taki m razie to świetna stronka bo już umiem...

Jakub: Dokładnie. Ten wykres jest parzysty.

Małgosia: Hej mam pytanie do Kuby, czy jakoś w wolnej chwili mógłbyś dodać parę zadań dot. parzystości i nieparzystości? pozdrawiam

Jakub: Muszę jeszcze znaleźć tę wolną chwilę. Spróbuję jednak dodać.

Małgosia: Oks, dziękuje.

Maja: skąd mam wiedzieć w zadaniu kiedy funkcja nie będzie ani parzysta ani nie parzysta ?

Jakub: Po prostu najpierw sprawdzasz, czy funkcja jest parzysta, a następnie czy jest nieparzysta.

Funckje: Po chuj, że tak powiem, w ogóle sprawdzać te parzystości?

Jakub: To jest podstawowa własność funkcji, którą później się wykorzystuje w masie wzorów i zastosowań praktycznych.

kinga72772: mam to w liceum na rozszerzeniu

piterek: Znalazłem też info że zawsze jest tak: Niech f1, f2 będą funkcjami parzystymi, a g1, g2; funkcjami nieparzystymi. Wtedy: f1 * f2 i g1 * g2 oraz f1/f2 i g1/g2; (tam, gdzie określone) są funkcjami parzystymi, f1* g1 oraz f1/g1; (tam, gdzie jest określona) są funkcjami nieparzystymi, f1 o f2, f1 o g1, g1 o f1; jest funkcją parzystą ( "o" jest tu złożeniem funkcji), g1 o g2 jest funkcją nieparzystą. Czy mam to przyjąć jako dogmat czy też można na to przeprowadzić dowód analityczny?

maria: co jeżeli jest funkcja przyrzta/nieparzysta, nieparzysta/parzysta, parzsta*nieparzysta? czyli np.|x|/x³ albo x²*x⁵

Jakub: Trudno tak uogólniać, bo to zależy do poszczególnych przypadków. Parzysta / nieparzysta jest zwykle nieparzysta np. |x|/x³. Podobnie nieparzysta / parzysta i parzysta * nieparzysta. Tak mi się wydaje, ale przydałoby się przeprowadzić porządny dowód.

M: