geek: Witam, mam pytanko odnośnie zadania 6. Nie trudno się zorientować, że trzeba tylko to spierwiastkować i jest tam wzór skróconego mnożenia, następnie otrzymujemy coś takiego:

a4 + b4		a4 + 2a2b2 + b4
	≥
2		4

Co daje nam:

a4 + b4		(a2 + b2)2
	≥
2		4

No i równoważność powinna być zupełnie inna (przynajmniej taki wynika z odpowiedzi CKE). Oni

	(a2 − b2)2
mają:		. Mógłby Pan mi nakreślić co zrobiłem nie tak, bądź czego nie
	4

dokończyłem Pozdrawiam

geek: Poprawka: powinienem napisać spotęgować(w drugim zdaniu)

Jakub: Jak ty znalazłeś tą stronę z rozszerzoną maturą poprawkową 2010? Tutaj linka nie ma https://matematykaszkolna.pl/strona/matura.html Dopiero dzisiaj ją dodałem na serwer, ale jeszcze żadne zadanie nie rozwiązane, więc nie linkowałem. Pytam, bo jestem bardzo ciekawy. Dobrze zacząłeś, dalej jednak trzeba było to pociągnąć w ten sposób

a4+b4		a4+2a2b2+b2
	≥		/*2
2		4

2a4+2b4		a4+2a2b2+b2
	≥
2		2

2a4+2b4		a4+2a2b2+b2
	−		≥ 0
2		2

2a4+2b4−a4−2a2b2−b2
	≥ 0
2

a4−2a2b2+b4
	≥ 0
2

(a2−b2)2
	≥ 0
2

Nierówność prawdziwa, bo kwadrat z dowolnego wyrażenia jest zawsze dodatni lub równy zero. CKE tam w mianowniku ma 4, ale to nic nie zmienia. Jak chcesz mieć 4 to podziel nierówność przez 2

geek: Aha, dziękuje za wytłumaczenie, a odnośnie tego jak znalazłem stronę to po prostu wpisać 2085 w url bo Pan dodaje to analogicznie . Nie wiedziałem jak dokończyć bo byłem ciekawy jaki wynik i zobaczyłem w arkuszu CKE takie o to rozwiązanie. Dziękuje i pozdrawiam.

geek: Znaczy 2585 pomyliłem się

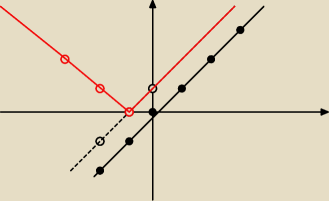
ADAM: A ja mam pytanie jak się rysuje wykres z podwójną wartością bezwzględną tj. y=IIx+3I−2I Wiem jak pozbywać sie podwójnej wartości bez.względnej w równościach i nierównościach ale to mnie zaskoczyło całkowicie. Ja to próbowałem zrobić tak, że 1.rysuje wykres y=x 2.przesuwam o v[−3,−2] 3.następnie odbijam od osiX może tak być?

ADAM:

Jakub: Źle robisz Adam y=IIx+3I−2I 1. Rysujesz y=x+3 2. Odbijasz część prostej pod osią Ox na górę i masz y=|x+3| 3. Przesuwasz o 2 w dół i masz y=|x+3|−2 4. Odbijasz część wykresu pod osią Ox na górę i masz y=||x+3|−2|

ADAM: Kolejny raz dzięki

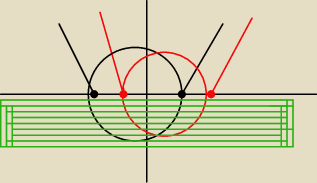
ADAM: Mistrzu czy mając zadanie narysuj wykres f(X)= Ix²−IxI−2I Moge zrobić tak że najpierw zakładam 1.IxI<o dlatego mam Ix²+x−2I rysuje i odbijam 2.IxI>0 dlatego mam Ix²−x−2I rysuje i odbijam I z tego mi wychodzą dwie parabole mające miejsca zerowe w −1, 2 i −2,1

Jakub: W zasadzie dobrze napisałeś, tylko pewnie chodziło ci w 1. x<0 a nie |x|<0 i tak samo w 2. Podsumuję: 1. dla x≥0 rysujesz x²−x−2, pogrubiasz część paraboli po prawej stronie osi Oy (bo robisz dla x≥0), a następnie część pod osią Ox tej pogrubionej części odbijasz nad. 2. dla x<0 rysujesz x²+x−2, pogrubiasz część paraboli po lewej stronie osi Oy (bo robisz dla x<0), a następnie część pod osią Ox tej pogrubionej części odbijasz nad. Całość tworzy wykres f(x) = |x²−|x|−2|

Jakub: Powstanie coś takiego http://www.wolframalpha.com/input/?i=f(x)%3D|x^2-|x|-2| Pierwszy rysunek jest powiększeniem drugiego, ale oba to wykresy f(x)=|x²−|x|−2|

ADAM: Dzięki Mistrzu!

ADAM: Mistrzu ostatnio przeglądałem informator z zadaniami do matury rozszerzonej i tam był bardzo proste zadanko Oblicz (√2−⁴√3−√2+⁴√3)² (napisałem przy trójkach pierwiastek z 4 ale w orginale były one pod podwójnym pierwiastkiem) i po zastosowaniu wzorów skróconego możenia wychodzi (√2−⁴√3)² − 2 √(2−√3)(2+√3) + (√2+⁴√3)² Przechodząc do sedna z (√2−⁴√3)² wyszło im 2−√3 A wg mnie tutaj (√2−⁴√3)² trzeba zastosować jeszcze raz wzór skróconego mnożenia, tak jak np tu https://matematykaszkolna.pl/strona/2602.html

Jakub: Po pierwsze √2 − ⁴√3 − √2 + ⁴√3 = 0, więc nie trzeba tego robić ze wzorów skróconego mnożenia. Chyba, że coś źle przepisałeś. To co napisałeś na końcu, ze wzoru skróconego mnożenia wygląda tak: (√2−⁴√3)² = (√2)² − 2*√2*⁴√3 + (⁴√3)² = 2 − 2*⁴√4*⁴√3 + √3 = = 2 − 2⁴√12 + √3 i tyle można uprościć

ADAM: http://www.zadania.info/d201/92507 Od razu pierwsze zadanie, wynik jaki jest tam podany to 2

Jakub: Czekaj. Robisz poważny błąd, przynajmniej tak mi się wydaje. Napisałeś, że √2−√3 = √2−⁴√3, czyli spierwiastkowałeś 2 i √3. To nie jest prawda Nie ma takiego wzoru. Gdyby to było mnożenie √2*√3 = √2*⁴√3 to ok, ale nie w dodawniu i odejmowaniu. Zresztą zobacz na takim przykładzie √9+16 = √9+√16 = 3+4 = 7 to jest jest błędnie, ponieważ √9+16 = √25 = 5 To zadanie zrobiłem na 2867. Tak z ciekawości, na zadania.info to zadanie jest rozwiązane z obliczeniami, czy tylko jest podany wynik?

ADAM: Jest zrobione z obliczeniami i wychodzi 2. Nie chciałem zapisać √2−√3 = √2−4√3 tylko nie wiedziałem jak zrobić żeby pierwiastek z 2 wchodził tez na √3. Miałem wątpliwości bo kierowałem się tym zadaniem https://matematykaszkolna.pl/strona/2602.html I chodziło mi czy nie trzeba było jeszcze raz zastosować wzoru skróconego mnożenia przy (√2−√3)² i (√2+√3)²

Jakub: Jeśli o to chodzi to do (√2−√3)² i (√2+√3)² trzeba stosować wzór skróconego mnożenia, aby to uprościć.

ADAM: Czy takie zadanie moze pojawić się na maturze rozszerzonej ? Punkt P jest pinktem wspólnym przekątnych trapezu ABCD, AB II CD, wektor−−> AB = [12,21] wektor−−>CB = [0,13] wektor−−>CP = [−3,−2] Oblicz współrzędne ABCD?

Jakub: Trzeba policzyć współrzędne wierzchołków trapezu. Tak? Mając same wektory nie obliczysz współrzędnych żadnego punktu.

ADAM: Tak, trzea policzyć wierzchołki trapezu ABCD, to zadanie jest z jednej matury rozszerzonej z 2011 link: http://www.zadania.info/d5/75823 zadanie 6 wczoraj męczyłem je godzine i nic nie mogłem sensownego obliczyć, dlatego zastanawiam się co w nim jest nie tak.

ADAM: Tam jest jeszcze podany punkt D =(10, −9)

Jakub: Wprowadź takie oznaczania: A = (x,y) B = (x+12,y+21) na podstawie AB = [12,21] C = (x+12,y+8) na podstawie CB = [0,12] P = (x+9,y+6) na podstawie CP = [−3,−2] Oblicz długość CP. Wyznacz współrzędne wektora PA, a następnie policz jego długość. Trójkąty ABP i PCD są podobne (odpowiednie kąty są równe). Znajdź skalę podobieństwa

	|CP|
k =
	|PA|

Współrzędne wektora DC = [x+12−10,y+8−(−9)] = [x+2,y+17] Wektory AB i DC są równoległe, więc dla wektorów DC = k * AB [x+2,y+17] = k * [12,21] x+2 = k * 12 i y+17 = k * 21 dalej już prosto To jest tylko schemat rozwiązania (podpowiedzi). Musisz to jeszcze porządnie zapisać.

ADAM: dzięki=)

lol: dz

maagduskaa: witam . ja mam pytanie czy istnieją matury poprawkowe z rozszerzenia? nie jest tak, że jeśli ktoś nie zda, to w najgorszym wypadku nie dostanie się na wymarzone studia? pzdr

Jakub: Gorzej. Jak ktoś nie zda, to obcinają nogi bez znieczulenia . A tak serio. Poprawek nie ma, bo matury rozszerzonej nie można nie zdać. Nawet jak dostaniesz 0, to i tak liczy się wynik na podstawie, jeśli chodzi o zdanie czy niezdanie.

Karolina: Aleeee, gdzie niby znaleźliście odpowiedzi do tej poprawkowej matury? Nigdzie nie ma..

Jakub: Klikaj niebieskie linki na poprzedniej stronie.

l;ll;: są poprawki rzozszerzonych!

pyt: prosta maturka, do napisania na 80% spokojnie