słaby matematyk ;/:
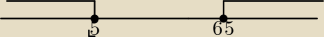
mi wyszło x1=−6,5 x2=−5 i nie rozumiem dlaczego 5 idzie w lewo a 6.5 w prawo
24 paź 12:49
słaby matematyk : juz wszytko rozumiem

24 paź 13:18
zaak: No właśnie dlaczego 5 idzie w lewo a 6,5 w prawo. Ktoś wyjaśni?
23 lut 14:47
Jakub: Na poprzedniej stronie jest na niebiesko x∊(−∞,5>u<612,∞). Kliknijcie. W ogóle wszystko co
niebieskie jest aktywnym linkiem do jakiegoś wyjaśnienia.
23 lut 16:26
olga : czy ja mogę to sobie obliczyć w taki sposób

?
log
3(2x−7)≤2−log
3(8−x)
log
3(2x−7)≤log
33
2−log
3(8−x) / + log
3(8−x)
log
3(2x−7)+log
3(8−x)≤log
33
2
log
3(2x−7)(8−x)≤log
33
2
(2x−7)(8−x)≤9
a drugi sposób
log
3(2x−7)≤2−log
3(8−x)
log
3(2x−7)≤log
33
2−log
3(8−x)
log
3(2x−7)≤log
33
2/(8−x) / *log
3(8−x)
log
3(2x−7)(8−x)≤log
33
2
24 kwi 17:36
Jakub: Pierwszy sposób jest dobry. Drugi jest zły, bo nie ma wzory na mnożenie logarytmów. W drugim
wierszu od końca mnożysz obydwie strony nierówności przez log3(8−x). Wykorzystujesz wzór
logax * logay = loga(xy) Taki wzór NIE ISTNIEJE. Nie można więc tak robić.
Jeszcze jedno. Nie można mnożyć nierówności przez log3(8−x). Mnożenie przez liczbę ujemną
powoduje odwracanie znaku nierówności. W przypadku log3(8−x) jest on raz dodatni raz ujemny.
Zależy od x. Tak więc nie wiemy, czy odwrócić znak nierówności czy nie.
Zawsze mnóż przez wyrażenie, co do których masz pewność, że są dodatnie lub ujemne dla
wszystkich x.
24 kwi 20:45
olga : a dziękuje bardzo

24 kwi 21:06
Marta: A czy można takim sposobem?:
log3(2x−7) ≤ log332 − log3(8−x)
log[3}(2x−7) ≤ log332/8−x
2x−7 ≤ 32/8−x /*(8−x)
(2x−7)(8−x) ≤ 9
−2x2 + 23x − 65 ≤ 0
28 sie 15:04
Jakub: | | 32 | |
Pisząc |
| powinnaś napisać, że to jest dla x≠8, co wynika z dziedziny. |
| | 8−x | |
(Mianownik musi być różny od zera).
Mnożąc w trzeciej linijce przez 8−x powinnaś napisać, że dalej nie odwracasz znaku nierówności
ponieważ 8−x>0. To wynika z dziedziny.
(Jak mnożymy nierówność przez liczbę ujemną odwracamy znak).
Te powyższe komentarze powinnaś napisać, bo inaczej można by się przyczepić do twojego
rozwiązania. Zauważ, że ja przenosząc log
3(8−x) na lewą stronę uniknąłem pisania tych
wszystkich komentarzy. Tylko po to zrobiłem i otrzymałem krótkie, eleganckie rozwiązanie.
28 sie 23:14
kojot: Dobra dobra a teraz mi z tym pomozcie bo czegos tutaj nie rozumie

! Ja zrobilem tak:
log
3(2x−7) ≤ log
39 − log3(8−x)
log
3(2x−7) ≤log
3(9/8−x)
opuszczamy logarytmy i wtedy bedzie:
2x−7≤9/8−x ( przy zalozeniu oczywiscie ze x jest rozne od 8)
2x−7 − 9/8−x≤0 (sprowadzamy do wspólnego mianownika)
(2x−7)(8−x)−9/(8−x)≤0
Na tym sie wykladam juz bo mnoze nawiasy delta wychodzi 17 niema pierwiastka i juz nie wychodzi
wiec pomozcie jak to dalej tym sposobem zrobic
17 lut 23:04
kojot: Dobra wyszlo mi to tym sposobem. Pomylilem sie w liczeniu delty
19 lut 16:00
xyz...: mi wyszło tak jak panu na samej górze. pierwiastki powinny wynosić−6 1/2 oraz −5 i wtedy
przedział to (−6 1/2, −5)
24 maj 20:10
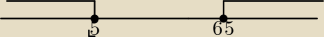 mi wyszło x1=−6,5 x2=−5 i nie rozumiem dlaczego 5 idzie w lewo a 6.5 w prawo
mi wyszło x1=−6,5 x2=−5 i nie rozumiem dlaczego 5 idzie w lewo a 6.5 w prawo

 ?
log3(2x−7)≤2−log3(8−x)
log3(2x−7)≤log332−log3(8−x) / + log3(8−x)
log3(2x−7)+log3(8−x)≤log332
log3(2x−7)(8−x)≤log332
(2x−7)(8−x)≤9
a drugi sposób
log3(2x−7)≤2−log3(8−x)
log3(2x−7)≤log332−log3(8−x)
log3(2x−7)≤log332/(8−x) / *log3(8−x)
log3(2x−7)(8−x)≤log332
?
log3(2x−7)≤2−log3(8−x)
log3(2x−7)≤log332−log3(8−x) / + log3(8−x)
log3(2x−7)+log3(8−x)≤log332
log3(2x−7)(8−x)≤log332
(2x−7)(8−x)≤9
a drugi sposób
log3(2x−7)≤2−log3(8−x)
log3(2x−7)≤log332−log3(8−x)
log3(2x−7)≤log332/(8−x) / *log3(8−x)
log3(2x−7)(8−x)≤log332

 ! Ja zrobilem tak:
log3(2x−7) ≤ log39 − log3(8−x)
log3(2x−7) ≤log3(9/8−x)
opuszczamy logarytmy i wtedy bedzie:
2x−7≤9/8−x ( przy zalozeniu oczywiscie ze x jest rozne od 8)
2x−7 − 9/8−x≤0 (sprowadzamy do wspólnego mianownika)
(2x−7)(8−x)−9/(8−x)≤0
Na tym sie wykladam juz bo mnoze nawiasy delta wychodzi 17 niema pierwiastka i juz nie wychodzi
wiec pomozcie jak to dalej tym sposobem zrobic
! Ja zrobilem tak:
log3(2x−7) ≤ log39 − log3(8−x)
log3(2x−7) ≤log3(9/8−x)
opuszczamy logarytmy i wtedy bedzie:
2x−7≤9/8−x ( przy zalozeniu oczywiscie ze x jest rozne od 8)
2x−7 − 9/8−x≤0 (sprowadzamy do wspólnego mianownika)
(2x−7)(8−x)−9/(8−x)≤0
Na tym sie wykladam juz bo mnoze nawiasy delta wychodzi 17 niema pierwiastka i juz nie wychodzi
wiec pomozcie jak to dalej tym sposobem zrobic