Gustlik: Czegoś tu nie rozumiem, Jakubie. Funkcja homograficzna ma być dopiero na studiach, choć to najprostsza postać funkcji wymiernej, a przesuwanie hiperboli jest na rozszerzeniu? Przecież hiperbola to wykres funkcji homograficznej i znajomość tej funkcji jest niezbędna do narysowania i przekształcania hiperboli. Jakoś nie wyobrażam sobie rysowania hiperboli bez omówienia własności funkcji homograficznej. To tak, jakbym chciał narysowac parabole nie znając funkcji kwadratowej.

Jakub: Faktycznie trochę to niekonsekwentne. Ale nic na to nie poradzę. Korzystam z aktualnych standardów maturalnych http://www.cke.edu.pl/images/stories/Inf_mat_08/mat_informator_10.pdf Tam po prostu nie ma słowa "homograficzna". Akurat to można szybko przeszukać. Prawdę powiedziawszy nie ma też sformułowania "funkcja wymierna". Są jednak "równania wymierne" i "wyrażenia wymierne" więc założyłem, że funkcja wymierna też jest obowiązkowa na podstawie. Funkcji homograficznej natomiast nie ma i trudno mi pisać, że jest. Niestety te standardy są dosyć nieprecyzyjnie napisane. Trochę się można domyśleć z przykładowych zadań, które zamieścili w dużej ilości. Jednak nie wszystkiego. Przesuwanie funkcji natomiast jest, więc pewnie też należy umieć przesuwać wykres funkcji wymiernej.

aga: Ktoś mi opisze i wytłumaczy jak się patrzy na własności funkcji homograficznej? proszę w poniedziałek mam prace klasowa!

Jakub: Zobacz rozwiązania zadań na tej stronie 1693.

olga: Panie Jakubie funkcja homograficzna jest w liceum oraz wiele innych rzeczy, które zaznaczyłeś na poziom studencki czy rozszerzenie, dlatego radziłabym nie patrzeć na standardy maturalne, bo dużo w nich nieścisłości tylko książki z matematyki do których na pewno masz jakiś dostęp, w nich jest wszystko.

miszczu: Racja zgadzam się z przedmówczynią

Jakub: Książki też są pisane według standardów. Problem polega na tym, że wiele książek na rynku jest napisanych według standardów na lata wcześniejsze. Z roku na rok materiał jest skracany i w tej chwili w księgarniach jest duży bałagan. Leżą jeszcze niesprzedane książki, które już są nieaktualne. Według standardów będzie układana tegoroczna (2010r.) matura. Cke musi tak postąpić, bo zaraz ktoś im wytknie, że dali zadania spoza obowiązkowego materiału. Już tak było w latach poprzednich, chociaż to były tylko małe odstępstwa. Zarzuty się jednak pojawiły i Cke musiało się bronić.

Flasiu: Chciałbym wtrąćić odlaczenie czarnej czcionki tego tematu. Taką funkcje miałem juz pod koniec 2 klasy Liceum

Myrthan: Mógłbym prosić jakieś zadania do tego przynajmniej dwa albo jedno, jeżeli to możliwe? : )

Jakub: Zobacz rozwiązania zadań na stronie 1693. To są dość typowe zadania na funkcję homograficzną.

ADAM: Co do standardów − ja jestem na ,,HUMANIE'' (co prawda będe pisał matematykę rozszerzoną) i u mnie w zakresie podstawowym F.homograficzna jest, była i będzie tak samo jak np. kwantyfikatory, moja nauczycielka zawsze mówi, że jakby miała uczyć wg standardów do nasza edukacja zakończyła by się na tabliczce mnożenia =)

Jakub: Ciesz się, że masz ambitną nauczycielkę. Wielu pedagogom się nie chce i ich wymagania kończą się na standardach.

ADAM: Dla mojej nauczycielki też pewnie by się nie chciało ale po 30 latach nauki w moim badź co badź jednym z najlepszych LO w kraju przejście z nauki rzeczy ,,przydatnych'' do ,,podstawy podstaw'' było by rzeczą trudną albo niemożliwą =) oczywiście ku mojej uciesze

maćko: Proponowałbym również umieścić na stronce wzory na asymptoty.... (które ów znalazły miejsce w moim podręczniku matematyki...)

	a
asymtota pozioma y =
	c

	d
asymptota pionowa x = −
	c

Strona jest niesamowicie przydatna dzięki Jakubie... (−;

Jakub: Dobry pomysł. Tylko należałoby jeszcze napis dodatkowy rozdział, co to są asymptoty z rysunkami i przykładami. Nie każdy wie. Do zrobienia w przyszłości.

slashuu matematyk: Witam jestem niezmiernie zadowolony z tej strony od 2 polowy 1 klasy liceum korzystam i ucze sie z niej aktywnie dzieki niej podnioslem swoje stopnie w szkole z matematyki , ale jest tylko jedna rzecz o ktora proszę ... WIECEJ ZADAN Z POZIOMU ROZSZERZONEGO

Seb: dołączam sie do tej prośby

zuza: Mam pytanie. Jak fukncje homograficzna z iloczynowej przekształcić do kanonicznej i na odwrót?

kladia: no dokładnie. Funkcja homograficzna i funkcja homograficzna z wartością bezwzględną jest w 2 LO. ja wlaśnie uczę się, bo jutro klasówka mnie czeka.

Daniel: Kuba, małe sprostowanie. Obecnie na podstawie przerabiamy funkcje homograficzną, tak więc zmień proszę status 'materiał ze studiów' na 'podstawę', czy co tam jest. To tak, aby potencjalna osoba, która nie jest do końca pewna, z czego ma się nauczyć na sprawdzian, nie zignorowała funkcji homograficznej jako 'aaa tam, to mają na studiach, to na pewno z tego nie będzie'. Wiesz o co chodzi . Pozdrawiam !

ebi:

Jakub: Daniel, zobacz informator maturalny. Tam po prostu nie ma określenia "funkcja homograficzna", "hiperbola". Akurat w pdf łatwo to przeszukać (Ctrl+f). Bierzesz to w szkole, bo albo nauczyciel jeszcze się nie przestawił na nowy program nauczania, albo chce wasz czegoś więcej nauczyć, oprócz podstawy. Do tego zresztą zachęca CKE.

Gustlik: Niektórzy nauczyciele używają nazwy "funkcja homograficzna", ale niestety nie wszyscy, nieraz muszę ucznia nauczyc tej nazwy. To jest TOTALNIE BEZ SENSU. Odnoszę wrażenie, że program nauczania został napisany na kolanach przez jakiegos miernego urzędniczynę z MEN, w dodatku nie bedącego matematykiem, a jeżeli był to matematyk, to baaaaardzo mierny. Bo prawdzwy matematyk by takiego bubla nie wypuścił.

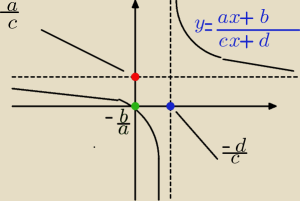
Gustlik: Najważniejsze własności funkcji homograficznej, które można odczytać ze wzoru:

	a
y=		+q
	x−p

1. Dziedzina: D=R\{p}. 2. Zbiór wartosci: ZW=R\{q}. 3. Współrzędne punktu przecięcia asymptot: W=(p, q). 4. Równania asymptot: pionowa x=p, pozioma y=q. 5. Wektor przesunięcia hiperboli: w^→=[p, q]. 6. Monotoniczność: gdy a>0 to funkcja malejąca w przedziałach x€(−∞, p); (p, +∞), gdy a<0 to funkcja rosanąca w przedziałach x€(−∞, p); (p, +∞), odwrotnie jak w przypadku funkcji liniowej. 7. Pozostałe własności, jak miejsca zerowe, punkty przecięcia wykresu z osiami, funkcja dodatnia i ujemna musimy wyznaczać tradycyjnymi metodami albo odczytywać z wykresu.

	2
Wyznaczę pierwszych 6 własności funkcji y=		+4
	x+3

Odczytuje ze wzoru: a=2, p=−3, q=4 1. Dziedzina: D=R\{−3}. 2. Zbiór wartosci: ZW=R\{4}. 3. Współrzędne punktu przecięcia asymptot: W=(−3, 4). 4. Równania asymptot: pionowa x=−3, pozioma y=4 5. Wektor przesunięcia hiperboli: w^→=[−3, 4]. 6. Monotoniczność: a=2>0 więc funkcja malejąca w przedziałach x€(−∞, −3); (−3, +∞),

	−5
Wyznaczę pierwszych 6 własności funkcji y=		−2
	x−4

Odczytuje ze wzoru: a=−5, p=4, q=−2 1. Dziedzina: D=R\{4}. 2. Zbiór wartosci: ZW=R\{−2}. 3. Współrzędne punktu przecięcia asymptot: W=(4, −2). 4. Równania asymptot: pionowa x=4, pozioma y=−2 5. Wektor przesunięcia hiperboli: w^→=[4, −2]. 6. Monotoniczność: a=−5>0 więc funkcja rosnąca w przedziałach x€(−∞, 4); (4, +∞),

	2x+3
Jeżeli funkcja jest podana w postaci ogólnej, np. y=		, to sprowadzamy ją do postaci
	x−5

kanonicznej: Dzielimy licznik przez mianownik, jak wielomiany: 2 −−−−−−−−−−−−−−−− (2x+3):(x−5) −2x+10 −−−−−−−−−−−− 13 Zatem funkcja ma postać:

	13
y=2+
	x−5

czyli

	13
y=		+2
	x−5

odczytuję ze wzoru: a=13, p=5, q=2 i ciąg dalszy jak w powyższych przykładach. Z takiej postaci można również łatwiej narysować wykres.

Gustlik: Wkradł się chochlik w 2 przykładzie, prawdopodobnie przez kopiuj−wklej: Powinno być tak: a=−5<0 więc funkcja rosnąca w przedziałach x€(−∞, 4); (4, +∞), ale obliczenia są poprawne.

Gustlik: Ze wzoru funkcji mozna jeszcze łatwo wyznaczyć środek i osie symetrii hiperboli.

	a
1) Hiperbola "nieprzesunięta", czyli funkcja y=
	x

środek symetrii: S=(0, 0) i pokrywa się z punktem przecięcia asymptot, osie symetrii: proste y=x i y=−x.

	a
2) Hiperbola "przesunięta", czyli funkcja y=		+q
	x−p

środek symetrii: S=(p, q) i pokrywa się z punktem przecięcia asymptot, osie symetrii: proste y=(x−p)+q i y=−(x−p)+q. Równania osi symetrii wzięły się z równania "kanonicznego" funkcji liniowej − prostej przechodzącej przez punkt P=(p, q). Funkcja ta ma postać y=a(x−p)+q, gdzie a − współczynnik kierunkowy prostej, ten sam, co w równaniu y=ax+b. Dla hiperboli współczynniki kierunkowe osi simetrii wynoszą zawsze a=1 i a=−1, stąd "brak" liczby przed nawiasem (x−p), natomiast obie osie musza przejść przez środek symetrii,czyli punkt S=(p, q). Np.

	3
y=
	x

Środek symetrii S=(0, 0) Osie symetrii y=x i y=−x

	4
y=		+3
	x−2

p=2, q=3 Środek symetrii S=(2, 3) Osie symetrii y=(x−2)+3 i y=−(x−2)+3, oczywiście opuszczając nawiasy można sprowadzić do równań y=ax+b. . .

Gustlik: Wierzchołki hiperboli. Nietrudno zauważyć, że jedna z osi symetrii hiperboli zawsze przecina obie gałęzie hiperboli "równo na dwie połowy". Jest to ta prosta, której współczynnik kierunkowy ma ten sam znak, co

	a		a
współczynnik a hiperboli y=		lub y=		+q. Druga z osi przechodzi zawsze "pomiędzy"
	x		x−p

gałęziami hiperboli. Wierzchołki hiperboli to nic innego, jak punkty wspólne hiperboli i osi symetrii przecinajacej hiperbolę. Wyznaczyć je można rozwiązując układ równań − hiperboli i osi przecinającej hiperbolę:

	a
− dla hiperboli "nieprzesuniętej" y=
	x

gdy a>0 − wybieramy równanie osi z dodatnim wspołczynnikiem kierunkowym:

	a
y=
	x

y=x gdy a<0 − wybieramy równanie osi z ujemnym wspołczynnikiem kierunkowym:

	a
y=
	x

y=−x

	a
− dla hiperboli "przesuniętej" y=		+q − podobnie:
	x−p

gdy a>0 − wybieramy równanie osi z dodatnim wspołczynnikiem kierunkowym:

	a
y=		+q
	x−p

y=(x−p)+q gdy a<0 − wybieramy równanie osi z ujemnym wspołczynnikiem kierunkowym:

	a
y=		+q
	x−p

y=−(x−p)+q Czyli prosta zasada: dodatnie a hiperboli − dodatni współczynnik kierunkowy prostej, ujemne a hiperboli − ujemny wspołczynnik kierunkowy prostej. Otrzymamy dwie pary rozwiązań (x₁, y₁) i (x₂, y₂), bo otrzymamy równanie kwadratowe. Te liczby będą współrzędnymi wierzchołków hiperboli. Np.

	3
1) Wyznacz współrzędne wierzchołków hiperboli y=		:
	x

Rozwiązujemy układ równań:

	3
y=
	x

y=x bo a=3>0, więc współczynnik kierunkowy również musi być dodatni.

	3
x=		/*x, x≠0 (dziedzina)
	x

x²=3 /√ x₁=√3, x₂=−√3, wstawiamy do któregoś z równan, najlepiej do liniowego: Zatem y₁=√3, y₂=−√3 W₁=(√3, √3), W₂=(−√3, −√3).

	−5
2) Wyznacz współrzędne wierzchołków hiperboli y=		:
	x

Rozwiązujemy układ równań:

	−5
y=
	x

y=−x bo a=−5>0, więc współczynnik kierunkowy również musi być ujemny. Dalej − analogicznie.

	3
3) Wyznacz współrzędne wierzchołków hiperboli y=		+2:
	x−4

Rozwiązujemy układ równań:

	3
y=		+2
	x−4

y=(x−4)+2 bo a=3>0, więc współczynnik kierunkowy również musi być dodatni.

	−4
4) Wyznacz współrzędne wierzchołków hiperboli y=		+3:
	x−5

Rozwiązujemy układ równań:

	−4
y=		+3
	x−5

y=−(x−5)+3 bo a=3>0, więc współczynnik kierunkowy również musi być dodatni.

	2x+3
Jeżeli funkcja jest dana w postaci "ogólnej", np. y=		to przekształcamy ją na
	x−4

kanoniczną, np. dzieląc licznik przez mianownik, jak wielomiany, (przykład w jednym z powyższych postów) będziemy wtedy mieli a, p, i q i potem już jest prosto.

Gustlik: Wkradł się chochlik w 2 przykładzie: Powinno być tak: bo a=−5<0, więc współczynnik kierunkowy również musi być ujemny oraz w 4 przykładzie: bo a=−4<0, więc współczynnik kierunkowy również musi być ujemny. Obliczenia są poprawne. To jest to, jak się robi kopiuj−wklej, czasem nie zauważy się, że coś jeszcze trzeba zmienić i skopiuje się z błędem

Anti:

	x
F(x) =
	4 − x

Oblicz argument, dla którego wartość funkcji F wynosi √3 i podaj go w postaci a + b√c gdzie a, b, c ∊ W i c > 0 czy ma ktoś pojęcie, jak to zrobić?... z góry bardzo dziękuję...

Jakub: Napisz to zadanie na forum zadankowym.

monika: ja to mam normalnie w lo..

Piotrek: Ludzie, ale Wy się czepiacie Jakub pisał już tyle razy, że robi to zgodnie ze standardami maturalnymi! Może i są one głupie no ale trudno taka była pewnie idea tej strony, więc ciężko teraz wprowadzać dużo zmian. Może w przyszłości będzie więcej. Ja też jestem po podstawie, a wszystkie te rzeczy brałem no, ale z tego można się chyba tylko cieszyć Teraz przeglądam to wszystko w ramach powtórki i jestem bardzo zadowolony, a jeżeli chce porobić coś więcej to zbiorek i jazda!

jaaaa: y=^2x_1+x² wartość najmniejsza i największa w przedziale <−2;2>

Marti: Funkcja homograficzna jest w moim liceum na wszystkich profilach w klasie 2 ... to nie material ze studiow ej...

buahahah: ⇔⇔⇔⇔⇔⇔⇔⇔⇔

edudamarek: http://matfiz24.pl Więcej o hiperboli i funkcji wymiernej dowiesz się na stronie.. Zapraszam Cię do VIDEO tłumaczenia zagadnień matematycznych. Pozdrawiam.

koknik: Ja mam funkcje homograficzną w liceum(mat−fiz), więc masz nieaktualną stronę niestety.

b156:

	−2x−7
Funkcja f określona jest wzorem f(x)=
	x+4

	k
a)przedstaw wzór funkcji F w postaci F(x)=		+Q a następnie podaj zbiór wartości
	x+p

funkcji F