Gustlik: Jakubie − ta sama prośba do Ciebie, co w przypadku funkcji wykładniczej. Czy mógłbyś napisać, jak przesuwa sie wykres funkcji logarytmicznej? Ta sama zasada, co w przypadku funkcji kwadratowej − przedstawia się funkcję logarytmiczną w postaci "kanonicznej", tj. y = log_a(x−p)+q i przesuwa o wektor [p, q], jak parabolę. Np. w przykładzie Ani należałoby narysować wykres funkcji f(x) = log x i przesunąć o wektor [1, −2], bo p=1, q=−2.

Jakub: Spróbuję w najbliższym czasie to dodać. Trochę roboty jest z tym rysowaniem wykresów, ale zabiorę się za to.

smutass: miały być wykresiki i nic

Tomek.Noah: Panie Gustlik jezeli zapiszemy f−cje logarytmiczna ogolnie czyli y=log_ax to translakja o wektor u[p,q] wyglada tak iz pierwsza wspolrzedna wektora odpowiada x a druga calego wyrazenia tak jest w kwadratowej wykladniczej i logarytmicznej zapewne czyli y=log_a(x−p)+q

lulu: Wie ktoś może jak się przesuwa wykresy ?

Gustlik: Tomek, o tym właśnie napisałem. Pozdrawiam.

aaa: Nie chce poganiać ale bardzo bym prosił o dodanie zadań z rozwiązaniami. Nie za bardzo rozumiem proces rysowania wykresy. Wiem tyle że trzeba wszystko ręcznie wyliczyć. dla liczb np od 0 do 6.

Karbon: Przy opisie wykresu jest błąd, powinno byc, że dziedzina= (0,∞) natomiast zbiór rozwiązań=R.

Jakub: Racja, przestawiło mi się miejscami. Poprawiłem. Dzięki.

Michał: mam taki problem z rozczajeniem wiec

	x
f(x)=log2
	1−x

D: x/1−x>0 x(1−x)>0 x₁ = 0 x₂ = 1 czyli x nalezy do przedziału (0:1) i wykres ma ramiona skierowane do góry. 2 przyklad. f(x)=log_x+1 (4−x²) dzidziwna wiadomo jaka bedzie bo to wiem no ale 4−x² >0

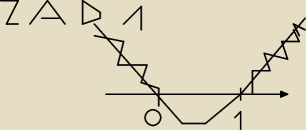
Michał: Michał: mam taki problem z rozczajeniem wiec x f(x)=log2 1−x x f(x)=log2 1−x D: x/1−x>0 x(1−x)>0 x1 = 0 x2 = 1 czyli x nalezy do przedziału (0:1) i wykres ma ramiona skierowane do góry. 2 przyklad. f(x)=logx+1 (4−x2) dzidziwna wiadomo jaka bedzie bo to wiem no ale 4−x2 >0 (2−x)(2+x)>0 x₁ =2 x₂ = −2 x należy do przedziału(−2;2) a wykres ma ramiona na dol

Michał: aaaa chyba za czailem tam gdzie jest np x² albo samo x i to jaki znak jest przed x to z tego sie wnioskuje jak beda ramiona hehe a to olsnilo mnie jak zle mowie to prosze mnie poprawic jak dobrze to pochwalic

Jakub: Zgadza się. Wykres f(x) = 4−x² = −x²+4 ma ramiona na dół, ponieważ przy x² jest minus, a konkretnie −1.

Kasia: Nie jest prawdą, że każdy wykres funkcji logarytmicznej przechodzi przez punkt (0,1). Np. y=log(x−3) +4 nie przechodzi przez punkt (0,1).

Jakub: http://pl.wikipedia.org/wiki/Funkcja_logarytmiczna Każda funkcja logarytmiczna ma równanie y=log_ax i każdy jej wykres przechodzi przez (0,1).

Marcinooo: Na sprawdzianie miałem takie zadanie : Narysuj wykres funkcji y=2^x oraz log2 x czy ktos potrafi rozwiazac to zadanie?

Kuba: Jakubie dziękuje <3

Filozof: dlaczego wykres funkcji log₃3x nie przecina się w punkcie (1,0) skoro każda funkcja logarytmiczna ma tam miejsce zerowe?

Jakub: Tylko funkcje logarytmiczne o wzorze y = log_a x przecinają oś Ox w (1,0). Funkcja y = log₃3x, ma inną postać i przecina oś Ox w (¹₃,0).

Piotr: Warto by dodać, ze wykres funkcji logarytmicznej powstaje poprzez symetrie ''y=x'' wykresu funkcji wykładniczej