Paweł: dlaczego liczysz wartość cos36*sin18 skąd to sie wzięło?

Jakub: Kombinując jak policzyć sin18^o zauważyłem, że jestem wstanie wyliczyć cos36^o*sin18^o na dwa sposoby. Czasami trudno napisać, co się skąd wzięło. Próbujesz, próbujesz na różne sposoby, aż wpadasz wreszcie na jakiś pomysł.

smutass: MASAKRA! weź wpadnij na to że akurat trzeba wziąść cos36sin18. Mam nadzieje, że na maturze takich rzeczy nie będzie.

Jakub: Zgadza się. Masakra. To jest bardzo trudne zadanie i na maturze raczej takiego nie będzie.

Tomek: Skomplikowany sposób, nie wiadomo czemu cos36sin18... Ja bym zrobił to w ten sposób: sin18 > x=18 > 5x=90 > 2x+3x=90 > 2x=90−3x sin2x=sin(90−3x) sin2x=cos3x , bo sin 90 zachodzi w kofunkcje czyli w cos 2sinxcosx=4cos³ x−3cosx 2sinxcosx−4cos³ x+3cosx=0 cosx(2sinx−4cos² x+3)=0 cosx=0 ∪ 2sinx−4cos² x+3=0 2sinx−4cos² x+3=0 > wystarczy cos zamienic na sin podstawic zmienną t i wychodzi ze sin18=−1+√5 / 4

Jakub: Dobry i dużo prostszy niż mój sposób Tomek. Gratulacje

Hans: Ja nie moge,jakie z Was mózgi są xD

visitor: z przecieków wiem, że ma być podobne na maturze rozszerzonej

Jakub: Daj linka do przecieków

Tomek: Witam, Jakub. sin 18 da sie obliczyc. Ale np. sin 22 albo tg 223 tez sie da obliczyc Masz na to jakis pomysł. W tablicach są podane wartosci kątów trygonometrycznych. Wiesz moze jak oni to liczyli

mojszesz: a ja bym to w ten sposób zrobił: Ojcze nasz, któryś jest w niebie, święć sięimi Twoje, przyjdź królestwo Tw.. oo sin18=−1+√5 / 4! dzięki Ci Panie!

ja: dlaczego 1/4sin(90⁰−18⁰)=1/4cos18⁰? to jest w liczniku na początku

ja: już wiem

Olek: cytuję sposób Tomka: "sin2x=cos3x , bo sin 90 zachodzi w kofunkcje czyli w cos 2sinxcosx=4cos³ x−3cosx" nie rozumiem co u Tomka stalo się pomiędzy tymi dwoma równaniami.. mógłby to ktoś wytłumaczyć? czy to ty Jakubie czy ty Tomku. a przdewszystkim skąd sie wzieło: 2sinxcosx=4cos³ x−3cosx?

xyzet: Wiem, że późno, ale może zajrzy tu ktoś z takim samym pytaniem Przekształcenie wynika z funkcji podwojonego i potrojonego kąta

ciekawsky: skad w jednym z wynikow 1/2?

Jakub: 2t−1 = 0 2t = 1 /:2 t = ¹₂ O tą ¹₂ chodzi?

Paul: Chodzi mi o samo działanie − 4t²( 2t − 1) + ( 2t − 1)² = 0 i jego przekształcenie w (2t − 1)(4t²+2t − 1) . W jaki sposób doszło do takiego przekształcenia? Prosiłbym przynajmniej o przekierowanie do odpowiedniego działu czy wzorów.

Jakub: To jest zwykłe wyciągnięcie wspólnego czynnika sumy przed nawias. Może rozpiszę to dokładniej: −4t²(2t−1) + (2t−1)² = −4t²(2t−1) + (2t−1)*(2t−1) = (2t−1)(−4t²+2t−1)

Ja: A ja to zrobilem tak: Sin18 = sin2*9(Sin2α) = 2*sin9*cos9 = 0.308, czyli wynik taki sam tylko w innej formie.

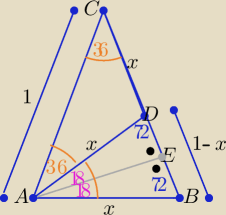
Eta: Podaję interpretacja geometryczną 1/Trójkąt równoramienny ABC o kątach 72^o, 72^o, 36^o i ramionach długości 1 ( co nie wpływa na wynik ) AD jest dwusieczną kąta 72^o, zatem trójkąt ADC jest równoramienny o ramionach "x" x∊(0,1) 2/ trójkąt ABD jest też równoramienny o ramionach "x" AE jest jego wysokością i i dwusieczną zatem dzieli kąt 36^o na kąty po 18^o stąd trójkąt ABE jest prostokątny i |AB|=x , |EB|= 1−x

	x		1−x
3/ z tw. o dwusiecznej:		=		⇒ x2+x−1=0
	1		x

Δ=5, √Δ=√5

	−1+√5		−1−√5
x=		v x=		<0 −−− odrzucamy
	2		2

	√5−1
x=		⇒ 2x= √5−1
	2

	|EB|		1−x		√5−1   1−   2		3−√5
sin18o=		=		=		=		=
	|AB|		2x		√5−1		2(√5−1)

	(3−√5)(√5+1)		−2+2√5		√5−1
=		=		=
	2*4		2*4		4

	√5−1
sin18o=
	4

Pozdrawiam

Jakub: Eleganckie i sprytne policzenie sin18^o z trójkąta

Kacper: Można też liczyć z ciągu Taylora Brooka. Im więcej wyrazów, tym lepsza dokładność wyniku. 1) 18° zamieniam na radiany: 18° = ^{18 * π}₁₈₀ rad = ^{18 * 3.14...}₁₈₀ rad = ^3.14...₁₀ rad ≈ 0.314 rad Swoją drogą 1 rad to ok. 57° 2) Teraz wzór ciągu (argument musi być w radianach): sin(x) = ^x1_1! − ^x3_3! + ^x5_5! − ^x7_7! + ^x9_9! − ^x11_11! ... Wzór to naprzemiennie dodatnie i ujemne stosunki potęg do silni kolejnych nieparzystych liczb naturalnych Uwaga! W obliczeniach korzystam z radianów, nie stopni: sin(18°) ≈ 0.314 − ^0.3143_3! + ^0.3145_5! − ^0.3147_7! = 0.314 − ^0.030959...₆ + ^0.003052...₁₂₀ − ^0.0003...₅₀₄₀ ≈ 0.314 − 0.005159... + 0.000024... − 0.000000... ≈ 0.308865 Podsumowując ^−1+√5₄ = 0.309016..., czyli powyższy ciąg na podstawie czterech pierwszych wyrazów, które liczyłem był dokładny do drugiego miejsca po przecinku. Można policzyć np. sin(17°), gdzie 17 nie ma zbyt wygodnych wielokrotności w celu policzenia wcześniej wspomnianym sposobem. Poza sinusem mogę wyliczyć dowolnego cosinusa używając wzoru jedynkowego.

Haiku: Eta Jeśli poprowadzisz wysokość trójk. ABC z wierzchołka C to masz od razu, że sin(18°) = x/2 a x obliczysz z: 1/x = x/1−x czyli x = −1±√5 /2 więc sin(18°) = x/2 = −1±√5 /4

Haiku: Oczywiście ujemny wynik odrzucamy bo α=18°