Dawid: Proponowałbym prostsze rozwiązanie tego zadania. Mianowicie chodzi mi o zastosowanie twierdzenia Pitagorasa do obliczenia długości boku kwadratu A: a²+a²=4² 2a²=16 a²=8 a=2√2 Myślę, że jednak łatwiejszy jest ten sposób Pozdrawiam

Jakub: Nie wiem, czy twój sposób jest łatwiejszy, ale mi się bardziej podoba . Ja wykorzystałem wzór na długość przekątnej d=a√2. Ty natomiast liczysz to z twierdzenia Pitagorasa. Twój sposób jest o tyle lepszy, że nie trzeba znać jeszcze jednego wzoru na długość przekątnej kwadratu.

big: przeciez to można policzyć bezpośrednio ze wzoru (d1*d2)/2

Jakub:

	d1 * d2
Oczywiście można policzyć to ze wzoru na pole rombu P =		. Chciałem jednak przy
	2

okazji pokazać, jak policzyć długość boku kwadratu.

d: mógłby mi ktoś napisać czym się rożni kwadrat wpisany a opisany?proszę bardzo,bo juz w tym wszystkim gubię...

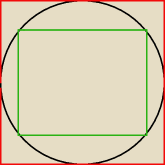
Jakub: Trochę niedokładnie, ale czerwony to kwadrat opisany na okręgu, a zielony to wpisany w okrąg.

d: dziekujea mógłbys mi jeszcze wytlumaczyc czym się różnia wzory na promien w kwadracie wpisanym i opisanym,proszę bardzo

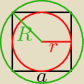
Jakub: a − długość boku kwadratu r = ¹₂a − promień okręgu wpisanego w kwadrat R = ¹₂a√2 − promień okręgu opisanego na kwadracie (połowa przekątnej kwadratu)

d: jesteś kochany,dziękuje Ci bardzo i przepraszam**

Czarna: Oblicz pole kwadratu wpisanego w okrąg . Promień okregu √2