ziomek:

	1
P=		a * h
	2

	1
PABC=		*4*2
	2

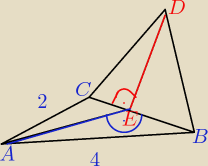
4 podstawa i 2 wysokość trójkąta ABC

	1
PCBD=		*2√5* |ED|
	2

2√5 podstawa i ED− wysokość trójkąta CBD Nie czaje ... dlaczego równanie złożone z tych pól i jego rozwiązanie przyczynia się do do tego że możliwe jest obliczenie wysokości |ED| W ogóle wolno zestawiać tak pola figur dajmy tej samej grupy (np trójkątny) w równanie gdy brakuje nam tylko jednego odcinka długości(składnika który jest nam potrzebny ) Pierwszy raz się z czymś takim spotkałem i dlatego nie bardzo rozumiem Ewentualnie mogę prosić o szersze/prostsze wytłumaczenie tego momentu w zadaniu.

ziomek: poprawka −literówka tam w nawiasie miało być trójkąty*

Jakub: Dobrze myślisz, że nie można tak po prostu przyrównać do siebie pól trójkąta ABC i CBD. Nie wiadomo czy są równe, raczenie nie są. Tylko, że ja tego nie robię. Zobacz na to równania: ¹₂ * 4 * 2 = ¹₂ * 2√5 * |AE| Po lewej stronie masz pole trójkąta ABC policzone w ten sposób, że bok AB (o długości 4) jest potraktowany jako podstawa, a bok AC (o długości 2) jest wysokością. W trójkącie prostokątnym przyprostokątne są pod kątem prostym, więc jeden z nich może być podstawą, a drugi wysokością. Po prawej stronie masz również pole trójkąta ABC policzone w ten sposób, że bok BC jest podstawą, a odcinek AE wysokością. Tak więc to równanie oznacza P_ABC = P_ABC, a to jest oczywiście prawda. To jest taki popularny trik na policzenie wysokości trójkąta prostokątnego poprowadzonej do przeciwprostokątnej. Inny sposób to z podobieństwa trójkątów ABC i AEC. Wtedy masz

AB		AE
	=
BC		AC

ziomek: właśnie tak myślałem, że z podobieństwa da się to policzyć. I chyba chyba tak zrobię, bo to rozumiem bardziej Ale dzięki za wyjaśnienie. Jeszcze jedno pytanie .. zanim będę wyliczać z podobieństwa to muszę założyć że jakaś figura "a" jest podobna do "b" (napisać "a" ~ "b" ? ) i póżniej wykazać że spełniają któryś z warunków podobieństwa?Pytam dla pewności , bo coś mi się obiło o uszy, że można na maturze dostać zero punktów jeśli poprawnie wyliczysz np dł. boku z podobieństwa bo zauważysz ,że są podobne figury a nie udowodnisz, że tak jest.

Jakub: Zgadza się, należy udowodnić, że trójkąty są podobne. Wystarczy pokazać, że mają takie same kąty. P_ABC ~ P_AEC, ponieważ 1. oba trójkąty są prostokątne, czyli mają po kącie 90^o. 2. kąt ACB trójkąta ABC jest równy kątowi ACE trójkąta AEC 3. trójkąty ABC i AEC mają odpowiednie dwa kąty równe, więc ich trzecie kąty też muszą być równe, ponieważ suma kątów w każdym trójkącie jest równa 180^o.

ania: dlaczego przy boku AE w mianowniku został √3 jak wiem w mianowniku nie może byc pierwiastków

roman: a ja na ten przykład nie ogarniam tego rysunku ....:(

Jakub: Pierwiastki mogą być w wyniku, tylko się przyjmuje, że takie wyniki są nieładne. Z tego powodu usuwa się niewymierność z mianownika, ale nigdzie nie jest powiedziane, że to jest obowiązkowe. Ja nie usunąłem, ponieważ ten bok AE był mi tylko potrzebny do policzenia ED. @roman Narysuj sobie kartce trójkąt prostokątny. Wierzchołek kąta prostego oznacz jako A, pozostałe wierzchołki jako B i C. Weź zapałkę. Postaw ją pionowo w punkcie A. Szczyt zapałki to będzie wierzchołek D. Taki ostrosłup ABCD powinieneś sobie wyobrazić patrząc na mój rysunek

roman: heh no ok juz mam dzięki

HMM: ciezko jest sobie wyobrazic,ze punkt E nalezy do wysokosci podstawy i wysokosci trojkata CDB