Gustlik: Często jest stosowana, zwłaszcza w analizie matematycznej funkcja wykładnicza y=e^x (e to podstawa logarytmu naturalnego, e=ok. 2,718). Funkcja ta ma tę ciekawą własność, ze jej pochodna y'=e^x i jest ona często wykorzystywana m.in. do badania przebiegu funkcji wykładniczych i logarytmicznych oraz w rachunku całkowym i różniczkowym.

Jakub: Pochodna funkcji e^x jest równa jej samej czyli e^x. To miał na myśli Gustlik, choć do końca tego nie napisał.

emce: ¹_√2−4^x

Gustlik: Jakubie, może warto byłoby wspomnieć o przesuwaniu wykresów funkcji wykładniczej? Obowiązują tutaj te same zasady, co przy przesuwaniu wszystkich innych wykresów funkcji, np. paraboli i hiperboli. Przedstawia się funkcję wykładniczą w postaci "kanonicznej", tj. y=a⁽x−p)+q i przesuwa o wektor [p, q], jak np parabolę. Np. wykres funkcji y=2⁽x−1)+3 możemy narysować przesuwając wykres funkcji y=2^x o wektor [1, 3], bo p=1, a q=3.

Jakub: Dobry pomysł. Postaram się dodać w najbliższym czasie.

albert: zastanawia mnie, dlaczego podstawa funkcji wykładniczej musi być większa od 0 ?

Jakub: Wzór funkcji wykładniczej to y=a^x. Zauważ, że gdyby np. a=−5 i x=¹₂ to mielibyśmy wtedy (−5)^1₂ = √−5 = ? Nie wolno pierwiastkować liczb ujemnych pierwiastkami parzystego stopnia. Dla uniknięcia takich kłopotów wprowadzono do definicji warunek a>0.

Tina: hej potrzebne mi są dwa zadanka 1 narysuj wykres funkcji a. y=−3^x b. y=3^x−2 −3 2. Omów własności funkcji z przykładu b.

Dywersant: Ale w funkcji wykładniczej, a może być 1, wtedy jest to funkcja stała. Takie założenie było w funkcji logarytmicznej, gdzie a musiało być różne od 1.

mam kolosa: a tutaj co napisal Gustlik,, y=2(x−1)+3 możemy narysować przesuwając wykres funkcji y=2x" to ta dwoja w pierwszym rownaniu to jest ta dwojka z drugiego rownania tak ? czyli do postaci wykladniczej bierzemy a czyli wspolczynnik kierunkowy normalnej postaci ? czy te a to po prostu taka zbieznosc nazw? a wie ktos moze jak skontaktowac sie z Gustlikiem , moze jakis blog czy cos, jezeli wyrazilby chec, bo wiem ze Jakub skupiasz sie na licealistach ale to i tak duuuuuzo

mam kolosa:

Jakub: Dwójka z y=2x to ta sama co jest w y=2(x−1)+3. Jeśli chodzi o postać wykładniczą, to nie bardzo rozumiem, o co ci chodzi. Może jakiś konkretny przykład. Z Gustlikem nie wiem jak się skontaktować. Często jednak bywa na forum zadankowym.

mam kolosa: ja rozumiem to tak: postac wykładnicza y=2^x funkcję wykładniczą w postaci "kanonicznej", tj. y=a(x−p)+q → y=2(x−1)+3 i teraz czy te dwojki z y=2^x i y=2(x−1)+3 to to samo, bo jezeli tak to znaczy ze 2 z y=2(x−1)+3 to wspołczynnik kierunkowy? no jakos tak mi sie w mojej malej glowie ułożyło i takie cos wyszło a co do Gustlika to ja myslalam ze masz kontakt na nk czy cos, ze go znasz tak bardziej prywatnie bo jak na nk, to ja w sumie tez na nk mogłabym sie skontaktowac zeby tak nie na forum

mam kolosa: bo ja sie teraz kuje z wstepu do matematyki z rodziny indeksowanej i ryk bo uwielbiam matematyke a nie che sie uczyc na blaszke tylko chce po prostu to rozumiec a tu miesza mi sie ilczyn czesc wspolna ze suma i ze niby wogole jaka rodzina

Jakub: Na pewno masz napisane y=a(x−p)+q, a nie y=f(x−p)+q Funkcja y=f(x−p)+q ma wykres funkcji f(x), tylko przesunięty o wektor [p,q]. Litery "a" w y=a^x i y=ax+b to jednak co innego. Matematyka na studiach na początku przytłacza, ale później jak się z nią oswoisz nie jest tak źle. Z Gustlikiem nie mam żadnego kontaktu, oprócz takiego, że sobie czasami dyskutujemy w komentarzach lub na forum.

Dżasta: Jakubie, gratuluję strony. Od kilku dni sumiennie ją ''studiuję''. Jest bardzo przejrzysta i można znaleźć wiele informacji To pomocne. Będę teraz regularnym gościem, bo w maju matura... pzdr

Madam Mi: Witam. Jakubie wytłumacz o co chodzi z tą funkcją wykładniczą? Ja naprawdę tego nie rozumiem.

Gofry: Nie wiem jak rozwiązać ale znam dobry przepis na gofry Składniki: 2 szklanki mąki 2 szklanki mleka 2 jaja 6 łyżek oleju 1 łyżeczka proszku do pieczenia Sposób przygotowania: Żółtka oddzielić od jaj. Zmiksować żółtka, mleko, mąkę, proszek do pieczenia, olej i sól na jednolitą masę. Białka ubić na sztywno i wymieszać z ciastem. Piec w rozgrzanej gofrownicy do osiągnięcia pożądanego koloru (na rumiano: 2−3 minuty) i podawać z ulubionymi dodatkami.

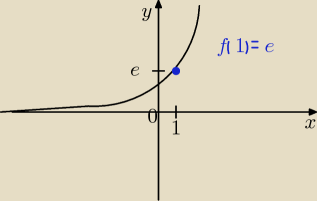
ebi: e^x = exp(x) zwana eksponentem przy okazji e ( 2,718...) ma inny zapis: e = 1+¹_1!+¹_2! + ¹_3! + ... = ∑^∞_n=1 (¹_n!) oraz e = l i m (1+¹_x)^x x∊ ℛ x→∞ jeżeli ktoś chce się więcej dowiedzieć o e , to proponuje książkę ,,Tajemnicza liczba e i inne sekrety matematyki" Bogdana Misia.

rogacz: wam się chce to liczyć?

ewusia: dlaczego ta funkcja f(x)=(2−√2)^x jest malejąca a ta funkcja f(x)=(3−√3^x jest rosnąca?

Jakub: Funkcja wykładnicza y=a^x jest malejąca dla 0 < a < 1 i rosnąca dla a > 1. f(x) = (2−√2)^x ≈ (2−1,41)^x = 0,59^x malejąca, bo 0 < 0,59 < 1 f(x) = (3−√3)^x ≈ (3−1,73)^x = 1,27^x rosnąca, bo 1,27 > 1

Rafio: Dzięki ebi za propozycję książki.