Majk: A nie lepiej skorzystać ze wzoru:
P=1/2(a+b+c+d)r

?
P=1/2 (5+5+5+5)*1
P=1/2 (20*1)
P=20/2
P=10 cm
2
5 sty 19:10
Jakub: Lepiej. Tylko to nie jest wzór ogólnie znany dla czworokątów. Dla trójkątów często się go
podaje, ale dla czworokątów to różnie. Na pewno nie ma go w tablicach rozdawanych na maturze
2009. Zauważ jednak, że mój sposób rozwiązania tak naprawdę sprowadza się do tego wzoru. Wziął
się on właśnie z takiego podziału figury na trójkąty.
8 sty 15:26
kinga: czy średnica koła wpisanego nie jest równa wysokości rombu?
wynikało by z tego, że pole można by policzyć po prostu ze wzoru P=a*h.
20 kwi 21:47
Jakub: Rzeczywiście jest. W sumie to tego nie zauważyłem, ale tak też można zrobić.
20 kwi 22:51
mm: Witam, a można korzystać z tego wzoru na pole czworokąta opisanego na okręgu jeśli nie ma go w
karcie wzorów?
4 maj 19:12
Jakub: Jak nie ma, to lepiej nie korzystać. To nie jest powszechnie używany wzór i sprawdzający może
uznać, że wystarczająco nie uzasadniłeś swojego rozwiązania.
4 maj 19:59
mst: Łatwiej jest tak:
a*h
5cm*2cm=10cm2.
1 mar 18:08
natalia: Witam
mam pytanie, chodzi mi o to, że romb ten został podzielony na 4 trojkąty prostokatne jednak
miedzi nimi znjaduje sie tez kawałek tego rombu. Pan liczy tylko pole tych trojkątów, a co z
reszta tego rombu , nie trzeba tego liczyć?
10 kwi 23:32
Jakub:
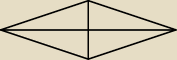
Chodziło mi o te większe trójkąty prostokątne. Te które masz na powyższym rysunku.
11 kwi 00:50
ktosiek: Ja policzyłem najpierw połowę drugiej przekątnej z trójkąta prostokątnego, wymnożyłem połówki
przekątnych razy 2, podstawiłem do wzoru d1d2/2 i wyszło mi 4√6, dlaczego?
27 kwi 22:08
Jakub: Co to jest druga przekątna z trójkąta prostokątnego?
28 kwi 00:40
ktosiek: Chodziło mi o to że podzieliłem romb na 4 trójkąty prostokątne o kątach prostych w przecięciu
się przekątnych, policzyłem z boku jednego z trójkątów prostokątnych połowę dłuższej
przekątnej, wymnożyłem ją razy dwa, wymnożyłem połówkę krótszej przekątnej razy 2 (bo połówkę
krótszej przekątnej znałem z promienia okręgu wpisanego) i podstawiłem do wzoru ef/2 i wyszło
mi tyle ile napisałem powyżej.
28 kwi 19:41
Jakub: Napisz może, w jaki sposób liczysz połowę dłuższej przekątnej. Domyślam, że robisz to z
twierdzenia Pitagorasa, ale jakie liczby podstawiasz?
29 kwi 18:26
ktosiek: Jeżeli zakładam że moje 4 trójkąty prostokątne mają kąty proste w przecięciu się przekątnych,
to jedną przyprostokątną jest promień okręgu wpisanego czyli r=1, przeciwprostokątną − bok
rombu a=5 i z tw. Pitagorasa liczę drugą przyprostokątną czyli połowę dłuższej przekątnej
e/2=√a2−r2.
29 kwi 22:38
Jakub: Chyba rozumiem, gdzie robisz błąd. Okrąg wpisany jest styczny do wszystkich boków, ale nie
przechodzi przez górny i dolny wierzchołek rombu. Przyjrzyj się dokładnie rysunkowi na
poprzedniej stronie. Górny wierzchołek rombu jest nad okręgiem. Minimalnie wystaje, ale jednak
nie możemy powiedzieć, że połowa krótszej przekątnej rombu jest równa promieniowi.
29 kwi 23:48
ktosiek: Aaa faktycznie.. dzięki, już rozumiem

30 kwi 00:11
madzia: wzor na pole a*h a wynosi 5 a h wynosi 2
28 gru 12:29
aa:

mam jedno pytanko: czy to też jest wliczone do pola tych trójkątów ?
28 kwi 18:42
aa:
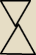
O coś takiego mi chodzi

28 kwi 18:43
Jakub: Tak to jest częścią trójkątów, których pola liczę.
29 kwi 22:23
bezendu:
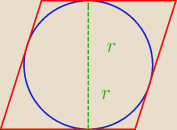
a nie prościej ?
r=1
h=2r
h=2
P=5*2=10cm
2
20 sie 23:20
Jakub: Prościej

Jakbym chciał się czepiać, to bym napisał, że trzeba udowodnić, że te dwa promienie
układają się w odcinek. Mogą przecież tworzyć kąt 179
o. Jednak to by było niepotrzebne
mieszanie. W zasadzie widać, że wysokość jest równa sumie dwóch promieni i to wystarczy.
22 sie 01:32
bezendu: 
24 sie 22:25
 ?
P=1/2 (5+5+5+5)*1
P=1/2 (20*1)
P=20/2
P=10 cm2
?
P=1/2 (5+5+5+5)*1
P=1/2 (20*1)
P=20/2
P=10 cm2
 Chodziło mi o te większe trójkąty prostokątne. Te które masz na powyższym rysunku.
Chodziło mi o te większe trójkąty prostokątne. Te które masz na powyższym rysunku.

 mam jedno pytanko: czy to też jest wliczone do pola tych trójkątów ?
mam jedno pytanko: czy to też jest wliczone do pola tych trójkątów ?
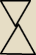 O coś takiego mi chodzi
O coś takiego mi chodzi 
 a nie prościej ?
r=1
h=2r
h=2
P=5*2=10cm2
a nie prościej ?
r=1
h=2r
h=2
P=5*2=10cm2
 Jakbym chciał się czepiać, to bym napisał, że trzeba udowodnić, że te dwa promienie
układają się w odcinek. Mogą przecież tworzyć kąt 179o. Jednak to by było niepotrzebne
mieszanie. W zasadzie widać, że wysokość jest równa sumie dwóch promieni i to wystarczy.
Jakbym chciał się czepiać, to bym napisał, że trzeba udowodnić, że te dwa promienie
układają się w odcinek. Mogą przecież tworzyć kąt 179o. Jednak to by było niepotrzebne
mieszanie. W zasadzie widać, że wysokość jest równa sumie dwóch promieni i to wystarczy.
