Daniel: wydaje mi się że jest bład ponieważ, z 2sin120 wyszlo 2sin60. wyglada jak blad w przepisaniu,
a moze czegos po prostu nie rozumiem

14 paź 22:41
Jakub: Skorzystałem ze wzoru
sin(180o − α) = sinα
i otrzymałem
sin120o = sin(180o − 60o) = sin60o
Wzory masz dostępne po kliknięciu niebieskiego > > nad znakiem równości.
16 paź 00:14
FKS_1939: takich wzorów w szkole nie przerabiałem to i może na maturze nie będzie takiego zadania
4 maj 18:49
Jakub: Pewnie miałeś wzór na pole trójkąta P=12absinα, gdzie kąt α jest między bokami a i b. W
karcie wzorów jest. Jeżeli się trafi ci się trójkąt rozwartokątny, gdzie α = 150o to będziesz
musiał policzyć sin150o. Zrobisz to za pomocą wzoru sin(180o−α) = sinα.
sin150o = sin(180o−30o) = sin30o = 12
Nawet na podstawie może się to przydać.
4 maj 20:15
Hanek.: A nie można innego wzoru na długość promienia okręgu opisanego na trójkącie, tj:
R=
2Pabc

9 cze 09:02
Jakub: Oczywiście można z tego wzoru Henek. Tylko musiałbym najpierw policzyć pozostałe dwa boki i
pole trójkąta. Zastosowany przeze mnie wzór jest prostszy.
9 cze 17:55
111: a skad wogle wzieło sie 2 sin α

bo 180−60−120 a nie 60
26 wrz 18:58
Jakub: Tam jest napisane na niebiesko "Korzystam ze wzoru na długość promienia okręgu opisanego na
trójkącie". Jak klikniesz, to zobaczysz z jakiego wzoru korzystam.
sin(180o−60o) = sin60o, ponieważ korzystam ze wzoru sin(180o−α) = sinα.
Kliknij niebieskie > >
3 paź 21:06
roman: chyba jest cos nie w tej kolejnosci zapisane przy rozwiazywaniu R ...
29 sty 22:40
Kamson:
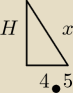
Ja zrobiłam to dzieląc trójkąt wysokością (otrzymałam trójkąt prostokątny 30,90,60) i
zamierzałam wyliczyć ze wzoru R=abc/4P. Ten trójkąt wygląda tak jak tutaj. Między 4,5 a x
jest kąt 30. Licząc z cos30 x=3
√3, a z sin30 H=3
√3/2 Licząc pole t. =27
√3/4.
R= 2*9*3
√3/4*4/27
√3 czyli pięknie się skróciło do 2 cm. Wiem, że to czasochłonne, ale w
wolnej chwili mógłby Pan mnie uświadomić co zrobiłam źle?

8 mar 23:43
Kamson: No nic, już rozumiem.
13 mar 18:35
Malineczka :):
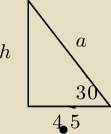
wiec
tg30=h/4,5
√3/3=h/4.5
h=4,5
√3/3
z racji ze R=2/3h to
R=2/3 * 4,5
√3/3 co daje 9
√3/9 gdzie 9 nam sie skroca i wychodzi piekne
√3
gdzie jest blad?!
15 mar 22:48
Jakub: Wzór R=23h obowiązuje tylko w trójkącie równobocznym. W innych, np. takim jak na
poprzedniej stronie, jest on fałszywy.
17 mar 01:03
gh: tgh
3 maj 12:36
Mumin: A nie zastanawiało was to, że promień tego okręgu jest o wiele mniejszy od połowy podstawy

Mnie również promień wynosi 2 cm, a długość podstawy tego trójkąta 9 cm. I jak go teraz
spróbować narysować w prawdziwych proporcjach

?
27 gru 22:47
Jakub: Promień okręgu to R = 3√3 ≈ 3 * 1,73 = 5,19 cm. To nie jest "wiele mniejsze" od połowy
podstawy czyli 4,5 cm.
27 gru 23:38
kasiula: dobrze jest Jakub zastosował wzory redukcyjne

one są na rozszerzeniu, ale podstawie
zdecydowanie się przydadzą przecież...

10 mar 20:56
mazur: to znaczy że to jest zadanie z zakresu podstawowego rozwiązane metodą z zakresu rozszerzonego

? i takie świństwo mogliby nam zrobić na maturze?
31 mar 20:06
ookamis: A czy to nie jest tak, że...
gdy okrąg jest opisany na trójkącie równoramiennym który przy podstawie ma kąty 30 (jak w
przykładzie) to promień okręgu jest zawsze równy ramieniu tego trójkąta?
I w tym przykładzie ramię jest równe 3
√3 tak jak promień. Promień rośnie razem z ramieniem.
| | a√3 | |
Wystarczyłoby obliczyć ramię (a) z równania 4,5 = |
| . Czy powyższe stwierdzenie jest |
| | 2 | |
prawdziwe?
3 sie 10:55
Jakub: Ciekawą zależność odkryłeś. Faktycznie jest tak dla trójkąta równoramiennego wpisanego w okrąg
i o kątach 30o przy podstawie, że długość jego ramienia jest równa promieniowi okręgu. Tylko
jest to bardzo mało znane twierdzenie. Ja np. o nim nie słyszałem. Sprawdziłem przed chwilą i
wiem, że jest prawdziwe, ale nie przypominam sobie, abym gdzieś o nim czytał. Na pewno nie ma
go też w spisie wzorów maturalnych. Oznacza to, że nie możesz się na niego powoływać. Możesz
co najwyżej na początku rozwiązania napisać to twierdzenie i je udowodnić. Jednak w ten sposób
nie otrzymasz krótszego rozwiązania, więc nie wiem, czy to ma sens.
Jednak jest to ciekawe i warto zapamiętać.
3 sie 14:27
Rafio: W teorii jest błędny wzór na promień okręgu z twierdzenia sinusów.
Alternatywnie zadanie można rozwiązać wyznaczając kąt środkowy oparty na tym samym łuku
co kąt wpisany α.
3 lut 16:57
Jakub: @Rafio Dziękuję, już poprawiłem wzór.
18 wrz 18:17


 bo 180−60−120 a nie 60
bo 180−60−120 a nie 60
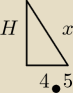 Ja zrobiłam to dzieląc trójkąt wysokością (otrzymałam trójkąt prostokątny 30,90,60) i
zamierzałam wyliczyć ze wzoru R=abc/4P. Ten trójkąt wygląda tak jak tutaj. Między 4,5 a x
jest kąt 30. Licząc z cos30 x=3√3, a z sin30 H=3√3/2 Licząc pole t. =27√3/4.
R= 2*9*3√3/4*4/27√3 czyli pięknie się skróciło do 2 cm. Wiem, że to czasochłonne, ale w
wolnej chwili mógłby Pan mnie uświadomić co zrobiłam źle?
Ja zrobiłam to dzieląc trójkąt wysokością (otrzymałam trójkąt prostokątny 30,90,60) i
zamierzałam wyliczyć ze wzoru R=abc/4P. Ten trójkąt wygląda tak jak tutaj. Między 4,5 a x
jest kąt 30. Licząc z cos30 x=3√3, a z sin30 H=3√3/2 Licząc pole t. =27√3/4.
R= 2*9*3√3/4*4/27√3 czyli pięknie się skróciło do 2 cm. Wiem, że to czasochłonne, ale w
wolnej chwili mógłby Pan mnie uświadomić co zrobiłam źle? 
 wiec
tg30=h/4,5
√3/3=h/4.5
h=4,5√3/3
z racji ze R=2/3h to
R=2/3 * 4,5√3/3 co daje 9√3/9 gdzie 9 nam sie skroca i wychodzi piekne √3
gdzie jest blad?!
wiec
tg30=h/4,5
√3/3=h/4.5
h=4,5√3/3
z racji ze R=2/3h to
R=2/3 * 4,5√3/3 co daje 9√3/9 gdzie 9 nam sie skroca i wychodzi piekne √3
gdzie jest blad?!
 Mnie również promień wynosi 2 cm, a długość podstawy tego trójkąta 9 cm. I jak go teraz
spróbować narysować w prawdziwych proporcjach
Mnie również promień wynosi 2 cm, a długość podstawy tego trójkąta 9 cm. I jak go teraz
spróbować narysować w prawdziwych proporcjach ?
?
 one są na rozszerzeniu, ale podstawie
zdecydowanie się przydadzą przecież...
one są na rozszerzeniu, ale podstawie
zdecydowanie się przydadzą przecież...
 ? i takie świństwo mogliby nam zrobić na maturze?
? i takie świństwo mogliby nam zrobić na maturze?