Ola: w jaki sposób została wyliczona dziedzina i zbiór wartości w tym przykładzie ? I po co są te, proste czerwone kreski na wykresie Pomocy

Ola: a i jeszcze skąd miejsce zerowe Jak je liczyć?

Jakub: Te czerwone proste to są asymptoty. Na czarnym wykresie rolę asymptot pełniły osie układu współrzędnych Ox i Oy. Na czerwonym wykresie musiałem je dorysować. Do asymptot wykres się zbliża, ale ich nie dotyka. Przykładowo im dalej w prawo tym bardziej czerwony wykres będzie się zbliżał do poziomej czerwonej asymptoty y=−1, ale jej nigdy nie dotknie. Dziedzinę odczytałem z wykresu. Czerwony wykres jest określony dla każdego x tzn. dla każdego x istnieje punkt oprócz jednego. Dla x = −3 masz pionową asymptotę i tak jak pisałem wyżej wykres się do niej zbliża, ale jej nigdy nie dotknie, czyli dla x = −3 wykres nie ma punktu, czyli liczba −3 wypada z dziedziny i to zapisałem: D = R \ {−3} − co oznacza: dziedzina = zbiór wszystkich liczb rzeczywistych oprócz −3.

ibot: otóż mam mały problem, powie mi ktoś jak obliczyć asymptotę ?

GRO: Ja asymptot nie liczę , nie wiem jak się je liczy ale wiem jedno , chociaż jest to błędem , jak narysujesz na końcu asymptotę to nic się nie stanie , chyba , że będziesz przy tablicy z tego odpowiadać.

GRO: Już znam odpowiedź , asymptoty to są tak jakby osie ox i oy , jeśli przesuwasz punkt o np. 3 jednostki w prawo , to cały wykres przesuwasz w prawo , jeśli w dół to cały wykres w dół , i ten drugi wykres co go narysujesz to asymptoty , warto zaznaczyć ją innym kolorem.

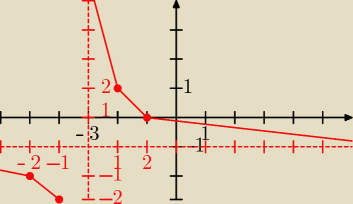
Gustlik: Można to zrobić bez rysowania dwóch hiperbol − narysować asymptoty, potraktować te asymptoty jak "nowy" układ współrzednych i odrysować hiperbolę od asymptot.

	a
Funkcja homograficzna w postaci kanonicznej: y=		+q
	x−p

1. Rysujemy asymptoty − są to proste o równaniach x=p, y=q, i zaznaczamy na nich jednostki, takie same jak na "głównym" układzie współrzednych. 2. Traktujemy te asymptoty jak "nowy" układ współrzednych i rysujemy hiperbolę od asymptot.

	2
y=		−1, czyli p=−3, q=−1, asymptotami sa proste x=−3, y=−1.
	x+3

	2
3. Rysujemy w "nowym" układzie współrzędnych wykres funkcji y=		.
	x

W ten sam sposób można rysować wykresy innych funkcji postaci y=f(x−p)+q przesuniętych o wektor [p, q], nawet takich, których wykresy nie posiadają asymptot. Zaczynamy zawsze od narysowania prostych x=p i y=q i te proste nam służą jako "nowy" przesunięty układ współrzędnych i w tym układzie rysujemy np. prostą, parabolę, hiperbolę, krzywą wykładniczą, logarytmiczną, sinusoidę itp. w zależności od rodzaju przesuwanej funkcji. I w tym "nowym" układzie współrzędnych rysujemy wykres funkcji y=f(x) w tej podstawowej, najprostszej postaci.

Anna: Trzeba rysować wszystko czy tylko ten przesunięty wykres żeby zdanie było zaliczone?

Jakub: Można narysować tylko przesunięty wykres, tylko jak to zrobić bez tego początkowego? Znaczy, da się, ale nie jest to łatwiej.

Anna: Dziękuję.

DuuuuuusssZZzeK: Ogólnie wykresy dużo łatwiej rysować rozpoczynając od wyznaczenia asymptot odpowiednio poizomej y gdy przesuwamy w górę lub w dół i pionowej x gdy w lewo i w prawo,po przesunięciu nowe wykresy nie mają prawa przeciąć tych asymptot