zuza: skoro ctg jest odwrotnością tg to czemu gdy ctg jest √2/3, tg nie jest 3/√2 ?

Jakub:

	3
Nie chciałem zostawiać wyniku w postaci		. Zwykle się usuwa niewymierność
	√2

(pierwiastek) z mianownika. Tak też zrobiłem. Jednak nie jest to konieczne, tylko lepiej wygląda.

SzymeQ: Nie wiem czemu utrudniacie sobie życie tak bardzo, oczywiście sposób dobry, ale dużo trzeba pisać. O wiele łatwiejsze jest narysowanie trójkąta prostokątnego zaznaczeniu α i policzenie z pitagorasa wszystkiego. Oczywiście możliwe jeżeli mamy podaną jedną z funkcji w postaci ułamka.

tymmi: dla mnie ten sposób jest szybszy, bo większość rzeczy obliczam w pamięci, wyciągam to w 8 linijek z których 1 to pierwsza funkcja, a 3 to rozwiązane pozostałe. czyli jednak szybciej napisać 4 linijki obliczeń niż bawić się w trójkąt, co?

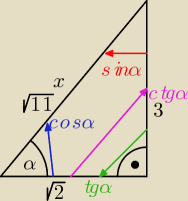
Gustlik: Szymek, jeżeli funkcja jest podana liczbą całkowitą, to robisz z niej ułamek o mianowniku 1,

	2
np. tgα=2=		i też można trójkątem.
	1

	√2
ctgα=
	3

x²=(√2)²+3² x²=2+9=11 /√ x=√11

	3		3√11
sinα=		=
	√11		11

	√2		√2*√11		√22
cosα=		=		=
	√11		11		11

	3		3√2
tgα=		=
	√2		2

gość: Skoro nasz ctg = ^√2₃ a ze wzorów wiemy, że ctg = ^cos_sin to czemu sin nie równa się 3 a cos nie równa się √2? Gdzie logika?

Jakub:

	cosα		√2		√2
Jak masz ctgα =		=		, to są różne rozwiązania dające
	sinα		3		3

przykładowo cosα = √2 i sinα = 3 ale także

	cosα		2√2		√2
cosα = 2√2 i sinα = 6, bo		=		=
	sinα		6		3

	√22		3√11
cosα =		i sinα =		, bo
	11		11

cosα		√22		3√11		√22		11
	= cosα : sinα =		:		=		*		=
sinα		11		11		11		3√11

	√22		√2 * √11		√2
=		=		=
	3√11		3√11		3

maturzysta:

	√2
ctgα=		więc przyprostokątne mają wartości a=√2 i b=3
	3

	1
tgα=
	ctgα

	1
tgα=
	√2/3

	3
tgα=
	√2

	3√2
tgα=
	2

Gdybym chciał odczytać wartości przyprostokątnych z przedostatniego wiersza obliczeń:

	3
tgα=
	√2

to byłyby to wartości prawidłowe, takie jak przy ctgα. Gdybym jednak chciał odczytać wartości przyprostokątnych z ostatniego wiersza obliczeń:

	3√2
tgα=
	2

to wartości te, byłyby różne od tych z ctgα, a zarazem nieprawidłowe. Obie pary przy zastosowaniu twierdzenia Pitagorasa dają różne wartości przeciwprostokątnej, przy czym pierwsza para daje wynik prawidłowy, tj. √11 W tym zadaniu były już niejako podane wartości przyprostokątnych, ale gdzie indziej, gdybym musiał dojść tych wartości po spojrzeniu na wartość tgα, to uzyskałbym wynik nieprawidłowy. Dlaczego tak jest?

Jakub: Nad twoim wpisem jest odpowiedź dla użytkownika gość, która dokładnie odpowiada na twoje wątpliwości. Nie lubię rozwiązań, takie jak podał Gustlik, ponieważ sugerują, że jak mamy np.

	√2
ctgα =
	3

to dla tego równania istnieje tylko jeden trójkąt prostokątny o przyprostokątnych √2 i 3 tak jednak nie jest. Istniej wiele par, dla który

	√2
ctgα =
	3

np. 2√2, 6 lub 3√2, 9 lub 4√2, 12 itd. To co łączy te pary to tylko ich stosunek, czyli

	√2
jak weźmiesz pierwszą liczbę i podzielisz przez drugą to otrzymasz
	3

Piszesz coś takiego ,,W tym zadaniu były już niejako podane wartości przyprostokątnych, ale gdzie indziej, gdybym musiał dojść tych wartości po spojrzeniu na wartość tgα, to uzyskałbym wynik nieprawidłowy.'' Właśnie do tego doprowadza sposób Gustlika. Masz w zadaniu np.

	1
tgα =
	3

i już wydaje ci się, że masz długości przyprostokątnych, a z twierdzenia Pitagorasa długość

	1
przeciwprostokątnej. To duży BŁĄD. Jak w zadaniu masz podane tgα =		, to
	3

przyprostokątne mogą się równać 1, 3 lub 2, 6 lub 3 lub 9 lub jakakolwiek para liczb byle ich

	1
stosunek był równy		.
	3

Nigdy nie rozwiązuj zadania, że z jednej funkcji trygonometrycznej i Pitagorasa od razu piszesz wszystkie długości boków trójkąta prostokątnego. Do policzenia tych długości potrzeba dodatkowych informacji i obliczeń.

maturzysta: Teraz już rozumiem. Chociaż w większości zadań rozwiązanych sposobem Gustlika wynik jest prawidłowy, to świadomość tego błędu faktycznie ma niebagatelne znaczenie. Zwróciłeś uwagę na sposób rozwiązywania podany przez Gustlika. Czy nie jest tak, że w zasadzie to rozwiązanie jest de facto błędne, chociaż prowadzi do prawidłowego wyniku? Aby je uprawomocnić, należałoby wartości funkcji 3 oraz √2 przemnożyć przez stałą liczbę całkowitą, oznaczając ją np. "a". Wtedy można je przypisywać do boków trójkąta jaki przedstawił Gustlik. Za zadanie otwarte rozwiązane sposobem Gustlika chyba nie dostaje się maksymalnej ilości punktów na maturze?

Jakub: To bardzo dobry pomysł, aby oznaczać długości boków jako √2a i 3a. Pokazujesz w ten sposób, że masz świadomość, że długości boków trójkąta mogą być różne, a tylko ich stosunek jest równy

√2
	. Przez pisanie tego ,,a'' rozwiązanie ani specjalnie się nie wydłuża ani nie
3

komplikuje, bo ,,a'' jest skracane w równaniu w pewnym momencie. Cała zaleta korzystania z Pitagorasa itd. pozostaje. Sposób Gustlika nie jest zły. Po prostu zabrakło zdania:

	√2
W dowolnym trójkącie prostokątny, w którym tgα =		, pozostałe funkcje trygonometryczne
	3

mają taką samą wartość, więc mogę rozpatrywać szczególny trójkąt prostokątny o przyprostokątnych o długościach √2 i 3 i na jego podstawie znaleźć pozostałe funkcje trygonometryczne. Niby oczywiste, ale dla uczniów już nie takie oczywiste i później dochodzi do pomyłek, o których pisałeś.