Grzesiek: takie pytanie z mojej strony skąd wiemy, że P(A/B) oraz P(A część wspólna B) są rozłączne

Jakub: A/B to różnica zbiorów A i B, czyli to co zostało ze zbioru A po usunięciu elementów, które znajdują się w zbiorze B. AnB to część wspólna zbiorów A i B. Wszystkie elementy części wspólnej należą do zbioru B, czyli żaden nie mogą należeć do A/B. Oznacza to, że A/B i AnB są rozłączne (nie mają wspólnych elementów). Zobacz też 1059.

olga : a jakby było P(B\A) ? to w jaki sposób to obliczyć?

Jakub: Jeżeli A⊂B, to P(B/A) = P(B) − P(A)

Norbert: Co oznacza ten kwadracik Jakub

Jakub: Domyślam się, że chodzi o kwadracik między A i B. Tam jest znak zawieranie się. Zbiór A zawiera się w B. Nie wszystkie przeglądarki go dobrze wyświetlają. Spróbuj zainstalować firefoksa. http://www.mozilla-europe.org/pl/firefox/

Grzegorz:

	1		1		1
Dla A\B można też od sumy a i b odjąć b		−		=
	2		3		6

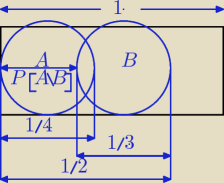
Gustlik: Cały prostokąt to Ω. P(A\B) można wyznaczyć geometrycznie − za pomocą rysunku: Z rysunku można obliczyć, że

	1		1		3		1		2		1
P(A\B)=P(A)−P(A∩B)=		−		=		−		=		=
	4		12		12		12		12		6

Beata: Czy w przypadku P(A∩B) mogę posłużyć się regułą mnożenia? tj. P(A∩B)= P(A) * P(B) wtedy P(A∩B)=1/4 * 1/3 = 1/12 Otrzymam ten sam wynik.