tiny_soul: zrobiłam to zadanie na zasadzie drzewka... i wyszły mi inne wyniki. z przekonaniem zrobiłabym to własnie tak... pytanie dlaczego mi wyszło inaczej?

Jakub: Trudno mi powiedzieć, dlaczego wyszło ci inaczej. Napisz swoje rozwiązanie. Oczywiście wynik rozwiązania zadania powinien być zawsze taki sam, niezależnie od wybranej metody.

asd: W punkcie a): dwóch kul białych na początku i czarnej na końcu... Czy jeśli zmienimy kolejność czarnej na początku i dwóch kul białych na końcu to będzie to samo? Niby tak bo z mnożenia wyjdzie to samo i prawdopodobieństwo też to samo, a jednak zmieniliśmy kolejność, która jest ważna.

Jakub: Jak zmienimy kolejność wynik wyjdzie ten sam, właśnie z tego powodu, że w regule mnożenia jest mnożenie , które jest przemienne. Jednak czarna na początku i dwie białe na końcu, to już inne zadanie, choć wynik ten sam.

Siemian: Ja bym prosił o jakieś uzasadnienie co do punktu b. Dlaczego obliczając dwie pozostałe kombinacje musimy korzystać z wariacji bez powtórzeń? Przecież zależy nam tylko na kuli środkowej, 1 i 2 nie powinny mieć żadnego znaczenia. Pozdrawiam

Jakub: W tym zadaniu robię to ze wzorów na wariacje bez powtórzeń, ponieważ w punkcie a) i b) mam pytania, w których kolejność jest ważna. Muszę więc także moc Omegi policzyć ze wzoru na liczbę wariacji bez powtórzeń, choć na pierwszy rzut oka chciałoby się to traktować jak kombinacje. Piszesz, że kule oprócz środkowej nie mają znaczenia. Jak najbardziej mają. Liczymy, ile jest pełnych zdarzeń elementarnych (trójek kul). To tak jakbyś na pytanie: "ile jest liczb dwucyfrowych parzystych?" odpowiedział: "jest ich 5, ponieważ jest pięć cyfr parzystych, a liczba dwucyfrowa parzysta musi się kończyć cyfrą parzystą, a pierwsze cyfry nie mają znaczenia". Odpowiedź oczywiście jest błędna. Jest więcej niż 5 liczb dwucyfrowych parzystych. Konkretnie 9*5=45. Pierwsza cyfra nie ma znaczenia, jeśli chodzi o to czy liczba dwucyfrowa jest parzysta czy nie, ale ma znaczenie, jeśli chodzi o ilość liczb dwucyfrowych parzystych. Tak więc, jak najbardziej musimy liczyć na ile sposobów możemy obsadzić pierwszą i trzecią kulę.

Siemian: Racja, dzięki.

?: aby obliczyć omegę to skąd wiedzieć czy brac wzór na kombinacje czy wariacje

Jakub: Na kombinacje brać, gdy kolejność nie jest ważna np. przy wyborze trzech osób z grupy. Na wariacje brać, gdy kolejność jest ważna np. przy ułożeniu liczby z trzech cyfr.

?: dzięki rozumiem, jednak trochę automatyczny jest dla mnie wzór na kombinacje− pasuje do wszystkiego

Somebody: Hmm w poprzednim zadaniu też losowalismy 3 kule i tam nie była ważna kolejnosć czyli C, a tu losujemy kule i jest ważna kolejność czyli V. A skąd ja mam wiedzieć, że tu jest ważna kolejność? Co mnie o tym informuje w treści zadania?

manti : Dużo łatwiej jest zrobić to metodą drzewka. Szkoda ze na stronce nie jest to w ogóle przedstawione.

xx: |Ω|=7*6*5=210, bo losujemy 3kule, a jest łącznie ich 7(4białe i 3 czarne). Więc pierwszą kulę losujemy na 7sposobów, drugą na 6, a trzecią na 5. a) pierwszą białą kulę losujemy na 4sposoby, drugą na 3sposoby, ostatnią czarną kulę losujemy na 3 sposoby (bo tyle jest kul czarnych). |A|=4*3*3=36. prawdopodobieństwo P(A)=|A|/|Ω|=36/210=6/35 b)pierwszą kulę(nie ma podanego koloru) można wylosować na 7kul−1kula czarna=6 sposobów, kulę czarną można wylosować na 3sposoby (bo są tylko 3 kule czarne), trzecią kulę można wylosować na 7−2poprzednie kule=5 sposobów |B|=6*3*5=90 P(B)=|B|/|Ω|=90/210=3/7

Mateusz: ja mam pytanie: Czy mozna to zrobic na zasadzie drzewka? Bo tej metody do konca nie rozumiem, a wyszlo mi tak samo...

Jakub: Można za pomocą drzewka. Jednak to będzie więcej roboty.

Wojtek: Mam pytanie czy w tym sposobie jest wliczone to ,że jako pierwsza zostanie wylosowana czarna kula i na drugie losowanie zostaną tylko dwie czarne kule ?

Jakub: Jeśli masz na myśli punkt b) to tak.

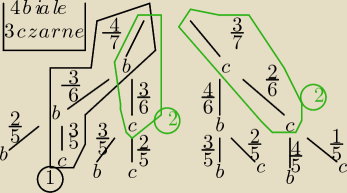
Osxx: a) P(1)= 4/7*3/6*3/5 = 6/35 b) P(2) = 3/6*4/7 + 2/6*3/7 = 2/7+1/7 = 3/7 Wyniki się zgadzają. Proszę wybaczyć niestaranność i bałagan .

nanana: mam pytanie, jeśli losuje 3 kule na raz to przecież kolejność nie ma znaczenia, zaś gdy losuje po kolei to ważne jest czy ze zwracaniem czy bez, a w tym zadaniu nie jest to uściślone, chyba, że to też nie ma znaczenia?

Jakub: W tym zadaniu jest losowanie bez zwracania. Zazwyczaj w zadaniu jest wyraźnie napisane, że chodzi o losowanie ze zwracaniem. Jak nie ma tego, to najczęściej chodzi o losowanie bez zwracania.