Lola: Czy schemat Hornera to sposób na znalezienie pierwiastków wielomianu?

Jakub: Schemat Hornera służy do dzielenia wielomianów. Jak dzielisz wielomian np. przez x−3 i nie wyjdzie reszta, to można powiedzieć, że 3 to pierwiastek. Tylko zamiast dzielić, dużo łatwiej jest sprawdzić bezpośrednio np. 5 jest pierwiastekiem wielomianu W(x)=x³−20x−3x−10, ponieważ W(5) = 5³−20*5−3*5−10 = 125−100−15−10 = 0 (wychodzi 0) O znajdowaniu pierwiastków poczytaj na stronie 1691

Tomek: Przy bardziej skomplikowanych wzorach lepiej użyć schematu bo uwierz mi , że często miejsca zerowe są ułamkami a nie pięknymi miejscami zerowymi

nat26: wydaje mi sie, ze w schemacie czy tez w tabelce Hornera powinna zachodzic taka przypadlosc ze w ostatniej wolnej runryce dolnego wiersza powinno zawsze wychodzic zero (0). a ty jakos inaczej to robisz? wiem o tej przypadlosci od wykladowcy z matematyki ze studiow. rozpatrz moj komentarz.

Jakub: Nie jest tak, jak piszesz nat26. W przykładzie z poprzedniej stronie, wielomian x³−4x²+3x−5 nie jest podzielny przez x−2, co oznacza, że wychodzi reszta. Mi wyszła reszta −7. Specjalnie dałem taki przykład. W ostatniej rubryce wyszłoby zero, gdyby x³−4x²+3x−5 był podzielny przez x−2, czyli liczba 2 byłaby pierwiastkiem wielomianu. Tak jednak nie jest 2³−4*2²+3*2−5 = 8−16+6−5 = -7 ≠ 0 (jak widać 2, to nie pierwiastek) Inna sprawa, że w typowych zadaniach szuka się najpierw pierwiastka, a następnie dzieli przez x−pierwiastek W rezultacie wychodzi w ostatniej rubryce zero i niektórzy błędnie przyjmują, że tak jest zawsze.

Wege: Za to w przykładach, ktore ja mialam na zajęciach (np Podziel wielomian W(x) = x³ + x² − 10x +8 przez dwumian (x−5)) i w pierwszej rubryce zawsze wychodziło 0, nie wiem tylko za bardzo dlaczego? To wynika akurat z takiego przykładu? I dlaczego skoro stała w dwumianie jest liczbą ujemną, pomnożyć trzeba przez jej dodatni odpowiednik?

kamil32213: proste jest młody

Michaił: A jeśli dzielimy np przez (x³−2x²+x−5) Jaką wartość przyjmuje wtedy c ?

Jakub: Za pomocą schematu Hornera można dzielić tylko przez wielomiany typu x+a lub x−a. Jak chcesz podzielić jakiś wielomian przez x³−2x²+x−5, to musisz to robić w ten sposób 107.

Gustlik: Ja to robię tak: 1 −4 3 −5 2 1 −2 −1 −7 Rysuję z przodu o jedna rubryke więcej niż Jakub, u góry pole jest puste, a na dole liczba z dzielnika spisuję pierwszy wspołczynnik wielomianu do drugiego wierza i potem u dołu mnożę i dodaję następna liczbę z góry, np. 2*1+(−4)=−2, 2*(−2)+3=−1, 2*−1+(−5)=−7

Gustlik: Odpowiadam na pytanie loli: mozna wykorzystać schemat Hornera do znalezienia pierwiastków wielomianu alternatywnie zamiast dzielenia przez dwumian i zdecydowanie polecam tę metodę bo jest duuuzo szybsza od dzielenia. Rozwiążę tu przykład Jakuba ze strony https://matematykaszkolna.pl/strona/133.html . x³−2x²−5x+6=0 Dzielniki 6: +−1, +−2, +−3,+−6 Schemat Hornera: 1 −2 −5 6 −1 1 −3 −2 8 ← W(−1)=−8, −1 nie jest pierwiastkiem 1 1 −1 −6 0 ← 1 jest pierwiastkiem Mam już jedno rozwiązanie x=1 (x−1)(x²−x−6)=0 Rozwiązuję funkcję kwadratową: Δ=(−1)¹−4*1*(−6)=1+24=25 √Δ=5

	−(−1)−5		1−5		−4
x1=		=		=		=−2
	2*1		2		2

	−(−1)+5		1+5		6
x2=		=		=		=3
	2*1		2		2

Rozwiązania to: x₁=1 v x₂=−2 v x₃=3

Gustlik: Errata: Δ=(−1)²−4*1*(−6)=1+24=25 wkradł się chochlik. Dalej jest dobrze, bo liczylem to jako (−1)².

kk: A jeżeli współczynnikiem przy najwyższej potędze nie jest 1?

kk: Ahaaa, już chyba rozumiem, zawsze przepisujemy pierwszy współczynnik, nawet jesli wynosi np. 23?

Gustlik: Tak, pierwszy współczynnik przepisujesz do dolnego wiersza.

aa: Gustlik, masz błąd w tabelce.

kasia: Rozwiązanie nierówności przy użyciu schematu hornera x³ +2x−3≥0 wyszły mi takie pierwiastki ale nie wiem co dalej ( x²+x+3(x−1) prosze o pomoc

Gustlik: Zasady rozwiązywania nierówności wielomianowych masz tutaj: https://matematykaszkolna.pl/strona/142.html . W pkl. 1 masz napisane: "rozkładam wielomian na czynniki", co oznacza, że mozesz zastosować każdą znaną Ci metodę rozkładu wielomianu na czynniki, którą można dany wielomian rozłożyć, aby tylko była poprawna, możesz więc rozłożyć również schematem Hornera. Pozostałe punkty bez zmian. Rozwiązane masz dobrze, z funkcji kwadratowej liczysz deltę: Δ=1−4*1*3=1−12=−11, czyli f. kw. nie ma pierwiastków, zatem wielomian ma tylko jeden pierwiastek x=1. Rysujesz oś, wykres od prawej strony z góry (a=1>0), przetnie oś w punkcie x=1 i pójdzie na dół, zatem x€<1, +∞)

oooo: a skad wiesz przez co podzielić wielomian

Jakub: To zależy od zadania. Na poprzedniej stronie pokazuję tylko jak podzielić za pomocą schematu Hornera.

backa: super wytłumaczony schemat Hornera czytając podręcznik nie mogłem się połapać o co chodzi

Ania: Błagam o pomoc! robię zadania tak jak jest wyjaśnione na tej stronie, ale nie wychodzą mi // i nawet nie wiem dlaczego... 1. (x³ − 2x + 1) : ( x−1) 2. (x⁴ − 6x +1): ( x −1) 3. ( x³ − 6x +1) : (x+1) 4. (x³ −2x +1) : (x−2) Oczywiście muszę zrobić to metodą Hornera...:( Proszę o pomoc, albo wskazówki.

Jakub: x³ − 2x + 1 = x³ + 0x² −2x + 1, do pierwszego wiersza tabelki wstaw współczynniki 1, 0, −2, 1 i powinno wyjść. x⁴ − 6x + 1 = x⁴ + 0x³ + 0x² − 6x + 1 x³ − 6x + 1 = x³ + 0x² − 6x + 1 x³ − 2x + 1 = x³ + 0x² − 2x + 1

kkkasiula: Widzicie ani 1 raz nie słyszałam o tym na fakultecie gdyby nie ta strona nie wiedziałabym jak to stosować dzięki Kuba i ja zrozumiałam wszystko na poprzedniej stronie w 100% mam nadzieje że to wystarczy i inne przykłady robi się analogicznie

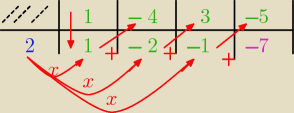
Gustlik: (x³−4x²+3x−5):(x−2) Robię o 1 rubrykę więcej niż Jakub,pierwsze pole u góry zamalowuję, bo ono pozostanie puste. A w drugim wierszu − pod pustym polem wpisuję miejsce zerowe dzielnika, czyli liczbę z dzielnika ze zmienionym znakiem, czyli 2, bo (x−2)=0 dla x=2. UWAGA ! Litera x przy łukach na rysunku oznacza mnożenie, a nie niewiadomą. W górnym wierszu wpisuję współczynniki wielomianu, potem pierwszy współczynnik spisuję "piętro niżej", a pozostałe obliczam wg schematu na rysunku. Wynik dzielenia to: x²−2x−1, bo schemat Hornera obniża stopień wielomianu o 1 ("środkowe" rubryki dolny wiersz), a reszta −7 − ostatnia rubryka u dołu. Czyli: (x³−4x²+3x−5)=(x²−2x−1)(x−2)−7

Mr. J: Wypadałoby zwrocić uwagę, że w przypadku dzielenia wielomianu np. x⁴−x²+17 trzeba go rozwijać do postaci x⁴+0x³−x²+17 bo niby wydaje się to oczywiste, ale nie raz można na tym stracić trochę czasu poprawiając błędy

Sonia: a jeżeli mam przykład (x⁵ − 8x⁴ + 16x³ + 2x² − 7x − 1 ) : (x² − 4x +1 ) da się to zrobic schematem hornera ? nie wiem jak zabrac sie za to , bo spotykalam same latwe przyklady typu (2x+1) a nie taki jak ten (x² − 4x +1 )

Grazie!: Dzięki za super−klarowne wytłumaczenie schematu! Rzeczywiście, to świetna metoda

MS: Czy na maturze jest obojętne czy podziele wielomian metoda "tradycyjna" czy poprzez użycie schematu Hornera?

Jakub: Tak. Obojętnie, którą metodą podzielisz wielomiany, abyś tylko otrzymał dobry wynik.