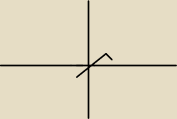
Beata: Witam,jeżeli wezme pnk −1,0,1,2 to wyjdzie taki wykres prowizorycznie,ale czy to bedzie dobry wykres do tej funkcji

Jakub: U ciebie wykres przechodzi przez punkt (0,0). W rzeczywistości, jak x=0, to nie jestem w stanie

	1		1
policzyć y=		, ponieważ nie wolno dzielić przez 0. Inaczej mówiąc, funkcja y=		nie
	x		x

ma wartości (punktu) dla x=0. To wyżej to tak przy okazji. Jeśli chodzi o twój problem, to narysowałaś wykres dla zbyt małej ilości punktów. Weź więcej. Zresztą rysując wykres funkcji najlepiej się zawsze domyślać jak on wygląda w rzeczywistości. Zobacz przykłady na stronie 157.

emes: dlaczego w tej funkcji przyjeto az tyle argumentów i po co te 1/2 ?

Jakub:

	1
Rysuję szkic wykresu y=		. Moim zdaniem to minimalna liczba x−ów, potrzebna do narysowania
	x

wykresu, który w miarę przypomina rzeczywistą hiperbolę. Przy mniejszej liczbie punktów, możesz po prostu źle je połączyć i zamiast hiperboli wyjdzie ci coś na kształt litery Z.

Natalia: a w tym przykładzie jak znaleźć argumenty jakiekolwiek

Jakub: Do tabelki wybierasz dowolne liczby. Takie, z których łatwo policzysz y ze wzoru y=¹_x.

Natalia: aha dziękuje

niekumata: nie rozumiem dlaczego przyjmujac dla x=1/2, wychodzi ze wzoru (y=1/x) ze y ma wartosc 2... przeciez 1/(1/2) to nie jest 2...

niekumata: przepraszam, chyba za duzo nauki na dzis 1/(1/2) to jest 2

ola: a dlaczego to ma być akurat hiperbola?

Jakub: Bo wykresem funkcji y=¹_x jest hiperbola. Zobacz 157.

Scofield: Przy takiej funkcji najpierw należy chyba wyznaczyć dziedzinę...