Illus: Skoro rzucamy kością 3 razy, to liczba sukcesów nie powinna równać się 3, a nie 2? Błąd, czy może ja czegoś nie rozumiem.

Jakub: Sukcesem w tym przykładzie jest wypadnięcie "piątki". Chcemy, aby "piątka" wypadła dwa razy w trzech rzutach. Tak więc liczba sukcesów k równa się 2. (k=2)

snelius: Przydałoby sie moze cos o histogramach rozkładu Bernoulliego tak zaciekawiło mnie ze schemat Bernoulliego jest materiałem ze studiów w szkole przerabiamy go na matematyce−profil mat−informatyczny mozna pisac tez ciekawe programy z zastosowaniem wzoru na liczbe sukcesów

?: czy mi się zdaje czy w pewnym mmencie prawdopodobieństwo sukcesu spada wraz z ilością rzutów?

Marek: Dobrze wytłumaczone. Bardzo się przydało . Jest wyjaśnione czytelnie i zrozumiale. Dziękuję, tego dokładnie szukałem − teraz można się tego nauczyć Już wiem jak rozwiązywać zadania tego typu.

ikaryy: to jest na rozszerzeniu

Adam: tylko ja mam to na matmie w liceum? (profil mat−fiz)

Jakub: W standardach nie ma tego na poziomie rozszerzonym, ani tym bardziej na podstawowym. CKE jednak zachęca nauczycieli, że jak mogą, to niech robią więcej niż w standardach, ponieważ w nich jest absolutne minimum. Widać masz szczęście mieć nauczyciela, który chce ciebie nauczyć trochę więcej, niż jest wymagane.

Marta: jak byłam na korkach do rozszerzenia to pani też mnie uczyła tego

Ania: "czy mi się zdaje czy w pewnym mmencie prawdopodobieństwo sukcesu spada wraz z ilością rzutów?" Spada, a bierze się to stąd, że tym wzorem liczymy prawdopodobieństwo *dokładnie* k sukcesów. Pozostając przy przykładzie kostki sześciennej, możemy sobie wyobrazić, że w czterech rzutach łatwiej jeden raz wyrzucić liczbę oczek, przyjmijmy, 5, niż w trzech rzutach, ale już przy 50 rzutach prawdopodobieństwo że *tylko 1 raz* wypadnie 5, jest bardzo małe

Robert: w technikum inf. też mam, a ten schemat, oprócz sposobu z drzewem jest jednym z najprostszych do rozwiązywania takich zadań

nosiema: http://tinyurl.com/wolframpisz tutaj widac jak zmienia sie prawdopodobienstwo dla liczby rzutow

Justyna : Hej ... dopiero zaczynam prawdopodobieństwo i nie rozumiem tego zapisu

k n
	− to jest silnia ale nie wiem jak to rozwiązać (chodzi mi o to jak rozpisać te liczby

żeby była ta silnia )

Jakub: Zobacz na 1014. Tę stronę masz także, jak klikniesz niebieskie > > na poprzedniej stronie. W ogóle klikaj wszystko co niebieskie .

Someone: Po co komu korki do rozszerzenia? Ta strona jest tak świetna, że bez problemu można z niej się do rozszerzenia solidnie nauczyć, chcieć to móc : ). Pozdrawiam Panie Jakubie.

źąbel: 1/6*1/6*5/6 + 1/6*5/6*1/6 +5/6*1/6*1/6 =5/216+5/216+5/216 = 15/216 = 5/72 bo liczba inna od piątki może być na 3 miejscach

Monika: Czy dałoby się to zadanie zrobić inną metodą?

Jakub: Zawsze się da inną metodą zrobić zadanie. Jednak należy wybierać tą najprostszą.

Karolina: Mam w zadaniu "rzucamy kostkami 3 razy, oblicz prawdopodobieństwo, że CO NAJMNIEJ DWA RAZY suma oczek...itd" to policzyłam najpierw prawdopodobieństwo, że pożądana suma wypadnie dwa razy, a potem osobno prawdopodobieństwo, że wypadnie trzy razy. I teraz nie wiem, czy mam te dwa prawdopodobieństwa dodać do siebie, czy pomnożyć przez siebie, żeby uzyskać końcowy wynik?

Zielona: W kazdej z trzech urn typu A znajdują się 4 białe, 3 czarne i 3 czerwone kule. W każdej z pięciu urn typu B znajdują się 2 białe, 6 czarnych i 2 czerwone kule. Losujemy 4 razy urnę (typu A lub B, każdą z prawdopodobieństwem 1\2 i za ka˙zdym razem z wylosowanej urny losujemy jedną kulę (po losowaniu kule zwracamy do urny). Jakie jest prawdopodobieństwo zdarzenia polegającego na tym, że a) co najwyżej dwa razy wylosujemy kulę białą, b) dok ladnie jeden raz wylosujemy kulę czerwoną, c) dok ladnie dwa razy wylosujemy kulę czarną? Ktoś pomoże? Tyle wiem że ze schematu Bernoulliego to ma być zrobione

Gustlik: Ja mam na to taki obrazowy sposób:

n k
	, bo na tyle sposobów mogę "rozmieścić" k sukcesów na n miejscach, czyli w n próbach,

reszte miejsc zajmą porażki. Możliwe są kombinacje np. SSPPSPPP, gdzie S to sukces, P − porażka p^k*q^n−k − bo prawdopodobieństwa pojedynczych zdarzeń, czyli sukcesów i porażek się mnoży ze sobą (reguła mnożenia). Ponieważ sukcesów jest k, więc prawdopodobieństwo sukcesu trzeba mnożyć k razy przez siebie, stąd p^k. Porażek jest reszta, czyli n−k, stąd q^n−k. To wszystko trzeba jeszcze pomnożyć przez liczbę konfiguracji, czyli liczbę rozmieszczeń k

	n k
sukcesów w n próbach opisaną na początku postu, czyli przez		, bo ta liczba to ilość

kombinacji k−elementowych z n. To tak, jakbym chciał k literek S (sukces) rozmieścić na n miejscach − muszę wylosować k miejsc z n dla literek S, pozostałe miejsca zajmą literki P (porażka). I stąd wzór na schemat Bernoulliego:

	n k
Pn(k)=		*pk*qn−k

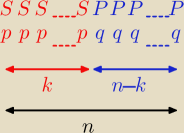
Gustlik: Litery S, P oznaczają odpowiednio sukces i porażkę. Liczby nad nimi to prawdopodobienstwa p i q. Liczby pod nimi to liczby sukcesów i porażek, czyli k i n−k ( u nas 2 sukcesy i 1 porażka) Liczba 3 na samym dole to liczba prób, czyli n. I teraz widać, co do czego podstawić: P₃(2)=

3 2		1		5		5
	*(		)2*(		)1=...=
		6		6		72

Gustlik: Należy pamiętać o jeszcze jednej rzeczy − zanim zaczniemy liczyć schemat Bernoulliego, należy rozpatrzyć pojedynczą próbę, czyli pojedyncze doświadczenie losowe, żeby ustalić prawdopodobienstwo sukcesu i porażki − p i q − ono odnosi sie zawsze do jednej proby, czyli do jednego losowania, rzutu kostka, monetą itp. Taką próbą Bernoulliego moze być proste zdarzenie, którego prawdopodobieństwo sukcesu i porażki można podać z głowy, jak np. rzut kostką, czy monetą, a czasem może być to bardziej skomplikowane zdarzenie, gdzie obliczenie p i q wymaga użycia klasycznej definicji prawdopodobienstwa, wzorów kombinatorycznych, a nawet drzewek. Np. może być takie zadanie: W urnie jest 10 kul, w tym 3 białe, a reszta to czarne. Losujemy jednocześnie 3 kule po 5 razy, każdorazowo zwracając je do urny. Jakie jest prawdopodobieństwo wylosowania 2 razy samych kul białych? I wówczas zanim zaczniemy liczyć schematem Bernoulliego musimy obliczyć p i q, gdzie p to prawdopodobieństwo wylosowania 3 kul białych, a q − prawdopodobieństwo zdarzenia przeciwnego. Mamy:

	10 3
|Ω|=		=120

	3 3
|A|=		=1

	1
p=P(A)=
	120

	119
q=P(A')=1−p=
	120

Teraz przystępujemy do schematu Bernoulliego: n=5 − bo tyle razy powtarzamy to losowanie k=2 − bo tyle razy chcemy osiągnąć sukces, czyli wylosować 3 kule białe (n−k)=3 − bo tyle razy musi nastąpić porażka w tej sytuacji

	1
p=		− prawdopodobienstwo sukcesu
	120

	119
q=		− prawdopodobienstwo porażki
	120

Podstawiamy do wzoru i liczymy:

	5 2		1		119
P5(2)=		*(		)2*(		)3=...
			120		120

Dalej nie będe liczył, bo będzie nieco zachodu, chciałem pokazać sposób dla wielokrotnie powtarzanych bardziej skomplikowanych zdarzeń niż rzuty kostkami czy monetami.

Patrycja: Myśliwy strzela do ruchomej tarczy w serii 20 strzałów. Jakie jest prawdopodobieństwo, że trafi co najmniej 3 razy, jeżeli prawdopodobieństwo trafienia do celu w pojedynczym strzale wynosi 0,6? Wskazówka: policzyć prawdopodobieństwo zdarzenia przeciwnego i odjąć je od 1! Myślałam, że będę umiała to rozwiązać, ale wychodzą mi kosmiczne liczby. Jeśli ktoś wie, jak to zrobić to bardzo proszę o rozwiązanie.

sdfsdfsdf: Patrycja, chyba chodzi o obliczenie sumy prawdopodobieństw na "sukcesy", czyli trafienia od 0 do 2 razy, a potem odjęcie tej wartości od 1 co da prawdopodobieństwo trafienia minimum 3 razy.

miecio: chyba zły przykład bo pierwszy udany rzut to 1/6 drugi udany rzut to 1/6 i trzeci nieudany rzut to 5/6 a to daje 5/216 porażka to nasz sukces 5/6 czy coś z moim myśleniem nie tak?

miecio: załapałem ale raczej chodzi tu o jeden rzut 3ma kostkami na raz to wtedy możliwości są 55X,5X5,X55 wtedy mamy 15/216 możliwości

Jakub: ,,bo pierwszy udany rzut to 1/6 drugi udany rzut to 1/6 i trzeci nieudany rzut to 5/6 a to daje 5/216'' Ale to tylko jedna możliwość otrzymania 5 oczek dokładnie dwa razy w pięciu rzutach. Możemy też otrzymać pierwszy rzut udany (1/6), drugi rzut nieudany (5/6), trzeci rzut udany (1/6) może też być pierwszy rzut nieudany (5/6), drugi rzut udany (1/6), trzeci rzut udany (5/6) Jak widzisz te udane i nieudane rzuty mogą przeplatać się w różny sposób. Ich liczba to

	n k		3 2
współczynnik		we wzorze Bernoulliego. W tym przykładzie równy		.