trygonometria ruper: Witam mam kolejny problem z rozwiazaniem zadania... polecenie brzmi. Oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego α jeżeli: a) tg α =3 b) sin α =³₄

TPB: W takich przykładach korzysta się z jedyni trygonometrycznej. Zrobię podpunkt a, bo jest ciut trudniejszy. a)

	sinα
tg α =		= 3
	cosα

sinα = 3cosα Jeżeli trójkąt α jest ostry, to wszystkie funkcje trygonometryczne są dodatnie. sin²α=9cos²α teraz korzystam z jedynki trygonometrycznej sin²α = 9(1−sin²α) 10sin²α = 9

	9
sinα =
	10

	3		3
sinα =		v sinα = −
	√10		√10

A jak stwierdziliśmy funkcje trygonometryczne są dodatnie, dla kąta ostrego

	3
Czyli sinα =
	√10

Teraz wyliczymy cosα, a to da się z jedynki trygonometrycznej sin^α+cos²α = 1

	9
cos2α = 1−
	10

	1		1
cosα =		v cosα −
	√10		√10

	1
Czyli cosα =
	√10

Teraz liczysz tangens i cotangens (to znaczy tangensa masz już obliczonego). A to idzie ze wzorów:

	sinα		cosα
tgα=		i ctgα =
	cosα		sinα

Pozostaje podstawić i obliczyć. Wyjdzie

	1
ctgα =
	3

ruper: bardzo skomplikowane....chyba sobie odpuszcze to zadanie

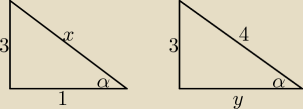Kozioł: a) x = √3² + 1² = √10

	3		3		3√10
sinα =		=		=
	x		√10		10

	1		1		√10
cosα =		=		=
	x		√10		10

	3
tgα =		= 3
	1

	1
ctgα =
	3

b) y = √4² − 3² = √7

	3
sinα =
	4

	y		√7
cosα =		=
	4		4

	3		3		3√7
tgα =		=		=
	y		√7		7

	y		√7
ctgα =		=
	3		3