Napisz wzór wielomianu W(x) w postaci iloczynowej Mickey: Wielomian W(x) ma trzy punkty wspólne z osią OX: (−4,0), (0,0), (1,0). Wiadomo, że nierówność W(x)>0 jest spełniona dla x in R − {1}. Napisz wzór wielomianu W(x) w postaci iloczynowej. Podpowiedź: Zastanów się jak przebiega wykres wielomianu, który spełnia nierówność. Jaki wpływ ma krotność pierwiastka na przebieg wykresu?

pomagacz: te punkty to są miejsca zerowe x₁ = −4 x₂ = 0 x₃ = 1 W(x) = (x + 4)x(x − 1)

Mickey: ale nie zgadza się to, że W(x)>0 dla wszystkich liczb rzeczywistych wyjątkiem 1. Przy tym wzorze W(x)>0 dla x należących (−4,0) suma (1,+nieskończ.)

Eta: błąd ,,,,,,,,,,,,,,, bo dla takiego W(x) >0 x∉R \ {1}

Eta: moja uwaga była skierowana do pomagacz

Mickey: yyy nie rozumiem...

Trivial: Dobrze przepisana treść zadania? Już na samym początku podajesz 3 punkty, które ∊ W. (−4, 0) → dla tego punktu nie jest wcale spełnione W(x) > 0, a x=−4∊R\{1} Chodziło o W(x) ≥ 0?

Mickey: treść zadania dobrze przepisana... też za nic mi nie może to wyjść...

Mickey: ale założmy że ma być W(x)≥0, jak to wtedy będzie?

Trivial: Wtedy tak samo, tylko że nie będzie spełniona dla x=1. Dziwne to zadanie. Ale chodzi im o to, żeby wiedzieć jak wygląda wykres taki np.: [x(x−1)(x+4)]². Być może czegoś tutaj nie rozumiem, ale wg mnie nie da się tego zadania rozwiązać.

Eta:

Trivial: Eto, wiesz jak to rozwiązać?

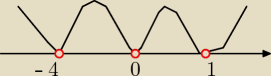
Eta: Nie ma takiej możliwości ........... cosik w treści nie pasuje może treść jest: w(x)>0 dla x€ R \ {−4,0,1} i wówczas uwzględniamy krotność ( dla wykładników parzystych) odp: np: W(x)=(x+4)⁴*x²*(x−1)²⁰ W(x)= (x+4)⁶*x⁵⁰*(x−1)⁴⁸ itd.............