Fajna planimetria dla chętnych.
Vax:
Fajna planimetria dla chętnych.
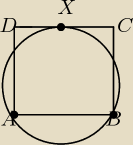
Dany jest kwadrat ABCD, X jest środkiem boku CD, na trójkącie ABX opisujemy okrąg, znajdź
długość promienia danego okręgu, wiedząc, że bok kwadratu ma długość a

19 sie 21:20
Jack:
| | 5a2 | |
R= |
|  (w sumie chyba proste, mogłem się walnąć w szybkich rachunkach) |
| | 8(2a−1) | |
19 sie 21:25
19 sie 21:29
Jack:
no i walnąłem − już widzę.
19 sie 21:29
19 sie 21:29
Eta:

19 sie 21:31
Vax: Eta dobrze

To może coś ciekawszego:
Dany jest kwadrat ABCD, punkty E i F leżą odpowiednio na bokach AB i BC w taki sposób, że BE =
BF, punkt X jest rzutem prostokątnym punktu B na CE, udowodnij, że na czworokącie CDXF da się
opisać okrąg.
19 sie 21:32
Jack:
te kąty mają 45o (∡D) i 135o (∡F) oraz 90o (∡C) i 90o (∡X). Stąd na czworokącie da się
opisać okrąg (45+135=2*90)− nie robię rysunku ale chyba jasne.
19 sie 21:45
Vax:
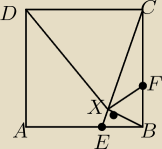
Nie do końca, może zrobię rysunek, żeby lepiej było widać o co chodzi

19 sie 21:54
Jack:
sorry, zaznaczyłem X na odcinku EF.... − "piłeś, nie prowadź"

19 sie 21:56
xXx: hmm to zadanie sprowadza się do pokazania, że ∡DXF=90
o 
myślę, myślę
19 sie 22:00
Gustlik: Oznaczam:
| | 1 | |
|AD|=|BC|a, |DX|=|CX|= |
| a
|
| | 2 | |
|AX|=|BX|=y − jest to trójkąt równoramienny
Liczę pole trójkąta ABX:
Widać, że podstawa jest równa a i wysokość h=a, zatem
Liczę boki trójkąta ABX
Korzystam ze wzoru na promień okręgu opisanego na trójkącie:
| | abc | |
R= |
| , gdzie a, b, c − boki trójkąta, P − pole trójkąta
|
| | 4P | |
| | √5 | |
u nas boki wynoszą a=a, b=c=y= |
| a
|
| | 2 | |
Odp:
20 sie 00:40
Gustlik: | | 1 | |
Uwaga: w mianowniku przy obliczaniu promienia wkradł sie chochlik: zamiast 4 |
| a2ma być
|
| | 2 | |
| | 1 | |
4* |
| a2, zgubiłem znak mnożenia, ale obliczenia są dobre. |
| | 2 | |
20 sie 00:43
Vax: Ja to zrobiłem trochę inaczej, oznaczyłem drugi punkt przecięcia BC z tym okręgiem jako Y i
| | a | | a2 | |
korzystając z twierdzenia o siecznej dostaję: ( |
| )2 = |
| = |CX|2 = |CY|*|CB| = |
| | 2 | | 4 | |
| | a | | √5a | | √5a | |
a*|CY| ⇔ |CY| = |
| , z twierdzenia Pitagorasa |BX| = |
| oraz |XY| = |
| i |
| | 4 | | 2 | | 4 | |
| | |XC| | | 1 | |
teraz w trójkącie XCB: sin CBX = |
| = |
| i na koniec z twierdzenia sinusów |
| | |XB| | | √5 | |
| | |XY| | | 5a | | 5a | |
w trójkącie BXY: 2R = |
| = |
| ⇔ R = |
| |
| | sin YBX | | 4 | | 8 | |
20 sie 01:01
AS:
| | a | |
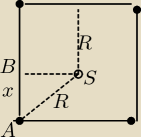
BS = |
| , x + R = a ⇔ x = a − R |
| | 2 | |
ΔABS − tw.Pitagoeasa
x
2 + (a/2)
2 = R
2
(a − R)
2 + a
2/4 = R
2
a
2 − 2*a*R + R
2 + a
2/4 = R
2
a
2 + a
2/4 = 2*a*R
20 sie 11:51
Vax: Tak, pozostało jeszcze 2 zadanie

20 sie 12:16
TPB: Analitycznie idzie nawet łatwo, ale nie brnąłem w to, bo byłby to dowód jak dla mnie za mało
elegancki, ale jak się poddam to będę jechał analitycznie, na razie główkuje nad czysto
geometrycznym sposobem.
20 sie 12:44
Vax: Analitycznie poszłoby nawet szybko ale masz rację, nie byłby to zbyt elegancki dowód

20 sie 12:49
TPB: Idę na dwóch pochodzić w kółko z kartką i długopisem, tak rozwiązuję geometrię

20 sie 12:50
TPB: No ja już rozwiązałem, ale mam pewną lukę w dowodzie. Próbuję dalej, może załatam tę dziurę.
20 sie 13:56
Vax: Ok, powodzenia

20 sie 13:57
TPB: Już mam, już pisałem dowód, kliknąłem backspace i mnie cofnęło z forum. jeszcze raz przepiszę,
chwilka.
20 sie 14:39
TPB: A więc mój dowód wygląda tak (a raczej szkic):
1. Na początku pokazujemy, że trójkąty prostokątne BEX, XBC iEBC są podobne. To jest chyba dla
wszystkich jasne. Wynika to z cechy kąt−kąt−kąt
2. Z powyższego podobieństwa wynika, że ∡XCD = ∡XBF=∡BEX
I teraz dochodzę do momentu gdzie się zaciąłem

3. Należy pokazać, że ΔBXF~ΔCXD
Z podobieństwa trójkątów prostokątnych z podpunktu 1 otrzymujemy równość:
Ale z założenia wiemy, że BC=CD (bo ABCd jest kwadratem) oraz EB=BF
stąd otrzymujemy
| BX | | BF | |
| = |
| czyli trójkąty są podobne (cecha bok−kąt−bok) |
| CX | | CD | |
4. Z udowodnionego przed chwilą podobieństwa, mamy równość miar kątów:
∡BXF = ∡CXD
| | π | |
5. Wiemy, że ∡BXF + ∡FXC = |
| , a stąd otrzymujemy równość: |
| | 2 | |
| | π | |
∡DXC+∡FXC = ∡BXF + ∡FXC = |
| |
| | 2 | |
Czyli
∡FXD jest prosty
6. Czworokąt można wpisać w okrąg wtedy i tylko wtedy gdy sumy przeciwległych kątów są równe
W naszym przypadku mamy ∡FXD+∡FXD = π, a więc również ∡XFC+∡CDX = π, bo suma miar kątów
wewnętrznych czworokąta jest równa 2π. Czworokąt CDXF można zatem wpisać w okrąg.
c.b.d.o
20 sie 14:52
Vax: Dobrze

20 sie 15:04
TPB: Uff ślepy geometrycznie jestem, zwłaszcza jak idzie o trójkąty podobne. Na każdym kroku
zapominam o tym jak wartościowe to narzędzie.
20 sie 15:07
Vax: Szczerze mówiąc ja mam podobnie, cały czas przerabiałem nierówności, ogólnie teorię liczb, ale
w końcu za planimetrię też się trzeba wziąć, na olimpiadzie nie ma tylko jednego działu

20 sie 15:09
TPB: Ja za miesiąc zaczynam studia, a zadanka olimpijskie dopiero po maturze zacząłem sobie
przerabiać. Takie to dziwaczne natręctwa mnie zaatakowały. Głównie nierówności, wielomiany,
teoria liczb... ale z geometrii to głównie robię zadania z gwiazdką podręczników, zestawów
maturalnych czy egzaminów wstępnych na wyższe uczelnie. Tam zawsze jak coś trzeba dowodzić w
tych zadaniach, to w 90% idzie z trójkątów podobnych, a ja siedzę nad zadankiem 3 godziny i
dopiero potem wracam do swojego pierwszego przeczucia. A do Om to owszem planometria to 25%
wszystkich zadań. Gdzieś na stronce był diagram procentowy udział różnych "działów" na OM.
Masz Prasolova, prawda?
20 sie 15:14
Vax: Tak, ostatnio trochę Prasolova przerabiam, tak poza tym to widziałem też Twój post na innym
forum matematycznym, gdzie o tym wspominałeś

20 sie 15:18
TPB: Hmm to nie mam chyba innych pdf−ów którymi bym się z Tobą podzielił.
A tak matematyka.pl zapomniałem, że mam tam konto

Ok ja lecę
20 sie 15:22
Vax: Btw. a na studia gdzie się wybierasz ?
20 sie 15:23
TPB: Studiować będę na Uniwersytecie Gagarina w Zielonej Górze
Aby tak ciekawy temat nie upadł to ja dodam pewne zadanko z planimetrii. W porównaniu do
poprzedniego dużo łatwiejsze.
| | 2 | |
W trójkąt równoramienny o obwodzie 40 cm wpisano okrąg, którego promień jest równy |
| |
| | 5 | |
wysokości poprowadzonej do podstawy. Obliczyć długości boków tego trójkąta.
A teraz zajmę się filmem, od dawna planowałem obejrzeć "Wujek Boonmee, który potrafi przywołać
swoje poprzednie wcielenia"
20 sie 17:33
xXx:
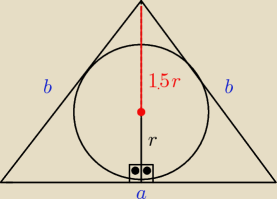
| | 2P | | (40−2b)*2.5r | |
(r= |
| ⇒ 2P=40r) ∧ (P= |
| ⇒ 2P=(40−2b)*2.5r) |
| | 40 | | 2 | |
| | 1 | |
(40−2b)*2.5r=40r / * |
| ⇒ 100−5b=40 ⇒ b=12 |
| | r | |
a=40−2b=16
a zatem boki tego trójkąta mają długości odpowiednio: 12, 12 i 16
20 sie 18:09
TPB: Dobrze

20 sie 18:11
TPB: To jeszcze jedno zadanie.
| | π | |
Dany jest równoległobok, w którym kąt ostry ma miarę |
| . Wyznacz stosunek długości boków |
| | 3 | |
| | 19 | |
równoległoboku, jeżeli stosunek kwadratów długości jego przekątnych jest równy |
| . |
| | 7 | |
20 sie 18:51
AS:
| | 2 | |
Dane: a + 2*b = 40 , r = |
| h |
| | 5 | |
20 sie 19:07
TPB: Ja zrobiłem to w ten sposób:
oznaczenia jak na rysunku xXx
P = 20r
P = U[1}{2}ah
a = 16
16+2b = 40 ⇔ b=12
20 sie 19:09
Vax:
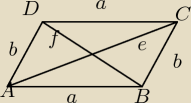
Z tw kosinusów:
f
2 = a
2+b
2−2ab*cos60 = a
2−ab+b
2
e
2 = a
2+b
2−2ab*cos120 = a
2+ab+b
2
Czyli z założenia dostajemy:
| 19 | | a2+ab+b2 | | (a/b)2 + (a/b) + 1 | |
| = |
| = |
| |
| 7 | | a2−ab+b2 | | (a/b)2 − (a/b) + 1 | |
19t
2−19t+19 = 7t
2+7t+7
12t
2 − 26t + 12 = 0
| | 2 | | 3 | |
t = |
| v t = |
| (w zależności czy a>b czy odwrotnie) |
| | 3 | | 2 | |
21 sie 01:53
TPB: Identycznie zrobiłem
21 sie 08:32
AS: W trójkącie prostokątnym przeprowadzono równoległą do przeciwprostokątnej
równą jednej przyprostokątnej.Kąt przeciwległy do tej przyprostokątnej = α.
W jakim stosunku zostało podzielone pole trójkata?
21 sie 11:02
TPB:
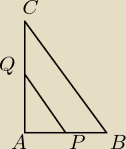
Wiemy, że AB=PQ oraz, że ∡ACB = α. Z faktu, że PQ i BC są równoległe, wynika, że
∡PQA = α oraz ∡APQ = ∡ABC. A więc trójkąty APQ oraz ABC są podobne.
| | AB | | PQ | |
sinα = |
| = |
| zatem skala podobieństwa wynosi k = sinα |
| | BC | | BC | |
Stosunek pól jest zatem równy
P
APQ = sin
2αP
ABC czyli P
PBCQ = cos
2αP
ABC
A stosunek pól tych figur jest równy tg
2α
21 sie 17:27
AS: Ok − uzyskałem taki sam wynik,tylko że znacznie dłuższą drogą.
Gratulacje.
21 sie 17:32
TPB: Dziękuję. To teraz ja się zrewanżuję.
W okrąg o promieniu długości 1 wpisano kwadrat oraz trójkąt równoboczny w ten sposób, że mają
wspólny wierzchołek. Oblicz pole części wspólnej obu tych figur.
21 sie 18:07
Vax: Również gratuluję

Fajnie, że zrobił się taki mały ,,łańcuszek" zadań z planimetrii, oby tak
dalej

To może ja zarzucę kolejne zadanko:
Dany jest trapez ABCD (AB i CD podstawy, |AB| > |CD|), niech X będzie środkiem podstawy AB, Y
środkiem podstawy CD, N punktem przecięcia przekątnych AC i BD, a M punktem przecięcia
przedłużeń ramion AD i BC. Udowodnij, że M,Y,N,X leżą na jednej prostej.
21 sie 18:10
TPB: To żeś Vax dowalił zadanie. Może tylko treść taka odstraszająca, ale dzisiaj mi się nie chce.
Może jutro powalczę z Twoim zadaniem.
Chociaż chwila, te wszystkie trzy proste to środkowe. A więc przecinają się w jednym punkcie,
czyli leżą na jednej prostej. W dobrą stronę idę?
21 sie 18:16
TPB: Zaraz wrócę to napisze swoje rozwiązanie...
21 sie 18:18
Vax: Ok
21 sie 18:18
Vax: Ja za 15min wychodzę i będę pewnie coś po północy.
21 sie 18:22
TPB: Jestem już. Ale cóż przemyślałem po drodze i odrobię się przeliczyłem. Bo przekątne AC i BD nie
będą środkowymi trójkąta ABM... pomyślę, może dam radę.
21 sie 18:30
TPB:
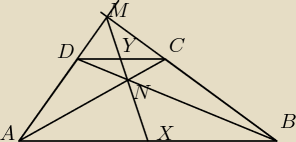
zadanie Vaxa:
Dowód:
∡CDM = ∡BAM
∡DCM = ∡ABM
∡DMC = ∡AMB
Zatem ΔDCM~ΔABM
Z podobieństwa powyższych trójkątów wynika, że MYX leżą na jednej prostej. Wystarczy pokazać,
że N należy do tej prostej. Albo inaczej, musimy pokazać, że przekątne trapezu oraz MX
przecinają się w jednym punkcie. Tutaj z pomocą przyjdzie nam twierdzenie odwrotne do tw.
Cevy. Informacje o tym możemy znaleźć w podręcznikach typowo olimpijskich. Mówi ono (to
odwrotne), że jeżeli
| AX | | BC | | MD | |
| * |
| * |
| = 1, to MX, AC i BD przecinają się w jednym punkcie (a to musimy |
| XB | | CM | | DA | |
udowodnić).
A więc powołując się na tw. Cevy. Uzyskujemy równość:
| BC | | DA | |
| = |
| , a to jest prawdą, bo ta równość wynika z twierdzenia Talesa. |
| CM | | MD | |
Zatem punkt N nalezy do prostej AX.
c.b.d.o
21 sie 18:52
TPB: To teraz daję swoje zadanie:
W okrąg o promieniu długości 1 wpisano kwadrat oraz trójkąt równoboczny w ten sposób, że mają
wspólny wierzchołek. Oblicz pole części wspólnej obu tych figur.
21 sie 18:53
21 sie 18:55
Vax: Prawie cały dowód ok, tylko zastanawia mnie implikacja, ΔDCM ~ ΔABM ⇒ MYX leżą na jednej
prostej, mamy pokazać, że odcinek MX przecina CD w połowie, nie jestem pewien, czy nie
| | DM | |
skorzystałeś tutaj z tezy. Można zauważyć, że ΔAXM ~ ΔDYM w skali k1 = |
| czyli |DY| = |
| | AM | |
| | MC | |
k1 * |AX| oraz ΔBXM ~ ΔCYM w skali k2 = |
| czyli |CY| = k2 * |BX|, ale z twierdzenia |
| | MB | |
Talesa k
1 = k
2, oraz |AX| = |BX|, czyli |YD|=|YC|.
22 sie 00:31
TPB: Też się zastanawiałem czy aby nie przeskoczyłem za szybko, ale jak zasypiałem to pomyślałem, że
mógłbym się tutaj bardziej rozwinąć.
∡DYM = ∡AXM oraz ∡DMY=∡AMY
Idziemy dalej. Wiemy, że DCM i ABM są podobne, oraz, że X i Y dzielą odpowiednie boki trójkątów
na połowy Prosta MY przecina CD pod tym samym kątem jak prosta MX bok AB, a ABIICD, zatem MYX
leżą na jednej prostej.
22 sie 07:41
Vax: Tylko cały czas wydaje mi się, że korzystasz z tezy. Mamy dowieść, że MYX są współliniowe,
można to zrobić albo jak opisałem wyżej, przyjmując, że Y jest punktem przecięcia MX z CD i
dowodząc, że wówczas Y jest też środkiem podstawy CD, albo przyjmując, że Y jest środkiem boku
CD i wtedy próbować dowieść, że odcinek MX przejdzie przez Y, ale w tym wypadku od razu odpada
nam równośc kątów ∠DYM = ∠AXM bo w tym wypadku musimy założyć, że MX przechodzi przez Y, a to
jest teza. Można by było napisać, że ∠AXM = ∠DKM, gdzie K jest punktem przecięcia MX i CD i
wtedy dopiero próbować dowieść, że K = Y. Mam nadzieję, że widzisz o co mi chodzi

22 sie 10:19
TPB: "Można by było napisać, że ∠AXM = ∠DKM, gdzie K jest punktem przecięcia MX i CD i wtedy dopiero
próbować dowieść, że K = Y. "
W sumie tak byłoby mi najwygodniej

.
Ale ciągle wydaje mi się, że jeżeli ΔDCM~ΔABM i MY (gdzie Y jest środkiem boku CD) przecina CD
pod kątem DYM równym AXM, to (gdzie X jest środkiem boku) to wynika, że AYM lezą na jednej
prostej. Chociaż nie wiem. Zamotałeś mnie. Ale generalnie pomysł, aby dowodzić, że K=Y wydaje
mi się najlepszy.
22 sie 12:15
Vax: Dobrze, to może tak, skąd wiadomo, że ∠DYM = ∠AXM ?

Jak z podobieństwa to napisz odpowiednie
równości kątów.
22 sie 12:17
Vax: Chodzi o to, że tak naprawdę teza sprowadza się do pokazania, że ΔDYM ~ ΔAXM, oczywiście mamy
dane ∠XAM = ∠YDM i zostaje pokazać równość ∠DMY = ∠AMX, a to już nie jest oczywiste, bo
właśnie tutaj zakładasz, że punkt M,Y,X są współliniowe, nie możemy tego założyć, odcinek MX
może przeciąć CD w jakimś innym punkcie K i wtedy M,K,X będą współliniowe, trzeba później
jeszcze dowieść, że punkt K leży na punkcie Y, a to w sumie sprowadza się do tego samego, co
udowodniłem wcześniej

22 sie 12:42
TPB: No właśnie zauważyłem już ten swój błąd.
22 sie 13:56
TPB: W okrąg o promieniu długości 1 wpisano kwadrat oraz trójkąt równoboczny w ten sposób, że mają
wspólny wierzchołek. Oblicz pole części wspólnej obu tych figur.
23 sie 08:50
AS: Coś brak chętnych do rozwiązania zadania.
Rozwiązałem problem,ale nie chce mi się piać,dużo rachunków.
Ustaliłem tryb postępowania prowadzący do rozwiązania.
24 sie 15:28
Godzio:
Jeszcze nie pisz rozwiązania, za jakieś 2 h pobawię się w to zadanie

24 sie 15:31
TPB: AS to napisz chociaż wynik to powiem czy dobrze.
25 sie 12:14
AS: Nie mam wyniku,opracowałem ścieżkę obliczeniową do wyniku.
Ja często tak robię nie chcąc tracić czasu na obliczenia,
wyznaczam kolejne etapy prowadzące do celu.
Bok taki a taki z trójkąta x tw.cos następny elemenr znowu z z czegoś itd.
25 sie 16:50
TPB: OK to daj chociaż skróconą ścieżkę swojego rozumowania i wrzuć swoje zadanko

25 sie 17:45
AS:
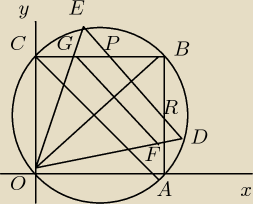
Promień okręgu:R , bok kwadratu: R
√2 , bok trójkata: R
√3
Pole szukanego obszaru: Pole ΔOGF + pole trapezu GFPR
Pole ΔOGF
Wsp.wierzchołków kwadratu
O(0,0) , A(R
√2,0} , B(R
√2.R
√2) , C(0,R
√2)
Równania boków kwadratu
OA: y = 0 , BC: y = R
√2 , OC: x = 0 , AB: x = R
√2
Równania boków trójkata ODE
OD: y = tg(15
0)*x , OE: y = tg(75
0)*x
Współrzędne wierzchołków trójkata OFG
F na przecięciu prostych AB i OD
OD: y = tg(15
0)*x , x = R
√2 , F(R
√2,R
√2tg(15
0))
G na przecięciu prostych OE i BC
OE: y = tg(75
0)*x , y = R
√2 , G(R
√2ctg(75
o),R
√2)
Długość odcinka OF
|OF|
2 = (Fx)
2 + (Fy)
2
Pole trójkąta OFG
Pole trapezu GFPR
Wsp. punktów D i E znajdziemy jako punkty wspólne prostych OD i OE
z równaniem okręgu o promieniu R
Wsp. punktu P znajdziemy z przecięcia się prostych BC i ED
Wsp. punktu R znajdziemy z przecięcia się prostych AB i ED
Wysokość trapezu w to odległość między prostymi GF i PR
26 sie 10:12
AS: Zadanie konstrukcyjne (łatwe)
Nakreślić konstrukcyjnie (tj przy pomocy tylko cyrkla linijki i ołówka)
trzy okręgi parami zewnętrznie styczne,znając położenie ich środków.
26 sie 10:17
TPB:
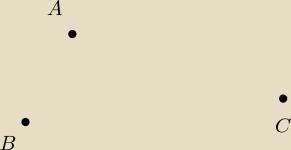
To znowu ja będę rozwiązywał zadanie. Szkoda, że taki fajniuśki temat umiera

Te trzy środki okręgów nazwijmy jako A,B,C (dla ułatwienia w taki sposób, aby |AB|≤|AC|≤|BC|).
Oznaczmy ponadto jako R
a,R
b,R
c długości promieni odpowiednio okręgów A,B,C. Oraz niech
Δl
1=|AC|−|AB| i Δl
2 = |BC|−|AC|. Nasze zadanie sprowadza się do wyznaczenia dł. powyższych
promieni, a to możemy zrobić rozwiązując układów równań:
| ⎧ | Ra+Rb = |AB| | |
| ⎨ | Ra+Rc = |AC| |
|
| ⎩ | Rb+Rc = |BC| | |
Odejmując drugie równanie od pierwszego ustalamy, że R
c=R
b+Δl
1
Odejmując trzecie od drugiego uzyskujemy R
b=R
a+Δl
2
Stąd R
c = R
1−Δl
1−Δl
2
Podstawiając R
b = R
a+Δl
2 do pierwszego równania otrzymujemy, że R
a = |AB|−Δl
2
Teraz przystępujemy do konstrukcji. Odmierzamy oczywiście odcinki AB,AC,BC,Δl
1Δl
2 dodajemy,
odejmujemy okreslone długości (to bardzo proste nie będę się tutaj rozpisywał) i otrzymujemy w
końcu długości promieni podanych okręgów.
29 sie 09:39
TPB: Dany jest trójkąt ABC, w którym kąt ACB ma miarę 600 oraz |AC|<|BC|. Punkt D leży na boku BC
przy czym |BD|=|AC|. Punkt E jest punktem symetrycznym do punktu A względem punktu C.
Udowodnić, że |AB| = |DE|.
29 sie 09:42
TPB: *Rc=Ra+Δl1+Δl2 (mały błąd)
29 sie 10:01
TPB: Zadanie dla chętnych:
Dany jest trójkąt ABC, w którym kąt ACB ma miarę 600 oraz |AC|<|BC|. Punkt D leży na boku BC
przy czym |BD|=|AC|. Punkt E jest punktem symetrycznym do punktu A względem punktu C.
Udowodnić, że |AB| = |DE|.
29 sie 10:02
AS:
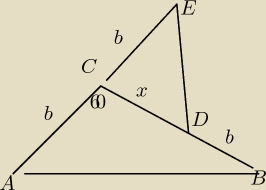
ΔABC: tw. cosinusów
AB
2 = (b + x)
2 + b
2 − 2*b*(b + x)*cos(60
o)
AB
2 = b
2 + 2*b*x + x
2 + b
2 − b
2 − b*x
AB
2 = b
2 + b*x + x
2
ΔDEC: tw.cosinusów
ED
2 = b
2 + x
2 − 2*b*x*cos(120
o) cos(120
o) = −1/2
ED
2 = b
2 + x*2 + b*x
Wniosek: |AB| = |BE| q.e.d.
29 sie 10:48
AS:
Zadanie konstrukcyjne (odświeżam,kiedyś już proponowałem,nikt nie rozwiążał)
Nakreślić konstrukcyjnie trójkąt,mając dane:
obwód trójkąta s oraz dwa kąty wewnętrzne α i β.
29 sie 10:52
TPB: Hmm pomyślę, może zrobię. Ale to najwcześniej 1−2 września, bo nie będę miał czasu wcześniej.
29 sie 12:30
 Fajna planimetria dla chętnych.
Dany jest kwadrat ABCD, X jest środkiem boku CD, na trójkącie ABX opisujemy okrąg, znajdź
długość promienia danego okręgu, wiedząc, że bok kwadratu ma długość a
Fajna planimetria dla chętnych.
Dany jest kwadrat ABCD, X jest środkiem boku CD, na trójkącie ABX opisujemy okrąg, znajdź
długość promienia danego okręgu, wiedząc, że bok kwadratu ma długość a 
 (w sumie chyba proste, mogłem się walnąć w szybkich rachunkach)
(w sumie chyba proste, mogłem się walnąć w szybkich rachunkach)
 To może coś ciekawszego:
Dany jest kwadrat ABCD, punkty E i F leżą odpowiednio na bokach AB i BC w taki sposób, że BE =
BF, punkt X jest rzutem prostokątnym punktu B na CE, udowodnij, że na czworokącie CDXF da się
opisać okrąg.
To może coś ciekawszego:
Dany jest kwadrat ABCD, punkty E i F leżą odpowiednio na bokach AB i BC w taki sposób, że BE =
BF, punkt X jest rzutem prostokątnym punktu B na CE, udowodnij, że na czworokącie CDXF da się
opisać okrąg.
 Nie do końca, może zrobię rysunek, żeby lepiej było widać o co chodzi
Nie do końca, może zrobię rysunek, żeby lepiej było widać o co chodzi 

 myślę, myślę
myślę, myślę





 3. Należy pokazać, że ΔBXF~ΔCXD
Z podobieństwa trójkątów prostokątnych z podpunktu 1 otrzymujemy równość:
3. Należy pokazać, że ΔBXF~ΔCXD
Z podobieństwa trójkątów prostokątnych z podpunktu 1 otrzymujemy równość:



 Ok ja lecę
Ok ja lecę


 Z tw kosinusów:
f2 = a2+b2−2ab*cos60 = a2−ab+b2
e2 = a2+b2−2ab*cos120 = a2+ab+b2
Czyli z założenia dostajemy:
Z tw kosinusów:
f2 = a2+b2−2ab*cos60 = a2−ab+b2
e2 = a2+b2−2ab*cos120 = a2+ab+b2
Czyli z założenia dostajemy:
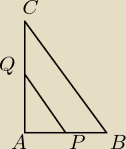 Wiemy, że AB=PQ oraz, że ∡ACB = α. Z faktu, że PQ i BC są równoległe, wynika, że
∡PQA = α oraz ∡APQ = ∡ABC. A więc trójkąty APQ oraz ABC są podobne.
Wiemy, że AB=PQ oraz, że ∡ACB = α. Z faktu, że PQ i BC są równoległe, wynika, że
∡PQA = α oraz ∡APQ = ∡ABC. A więc trójkąty APQ oraz ABC są podobne.
 Fajnie, że zrobił się taki mały ,,łańcuszek" zadań z planimetrii, oby tak
dalej
Fajnie, że zrobił się taki mały ,,łańcuszek" zadań z planimetrii, oby tak
dalej  To może ja zarzucę kolejne zadanko:
Dany jest trapez ABCD (AB i CD podstawy, |AB| > |CD|), niech X będzie środkiem podstawy AB, Y
środkiem podstawy CD, N punktem przecięcia przekątnych AC i BD, a M punktem przecięcia
przedłużeń ramion AD i BC. Udowodnij, że M,Y,N,X leżą na jednej prostej.
To może ja zarzucę kolejne zadanko:
Dany jest trapez ABCD (AB i CD podstawy, |AB| > |CD|), niech X będzie środkiem podstawy AB, Y
środkiem podstawy CD, N punktem przecięcia przekątnych AC i BD, a M punktem przecięcia
przedłużeń ramion AD i BC. Udowodnij, że M,Y,N,X leżą na jednej prostej.
 zadanie Vaxa:
Dowód:
∡CDM = ∡BAM
∡DCM = ∡ABM
∡DMC = ∡AMB
Zatem ΔDCM~ΔABM
Z podobieństwa powyższych trójkątów wynika, że MYX leżą na jednej prostej. Wystarczy pokazać,
że N należy do tej prostej. Albo inaczej, musimy pokazać, że przekątne trapezu oraz MX
przecinają się w jednym punkcie. Tutaj z pomocą przyjdzie nam twierdzenie odwrotne do tw.
Cevy. Informacje o tym możemy znaleźć w podręcznikach typowo olimpijskich. Mówi ono (to
odwrotne), że jeżeli
zadanie Vaxa:
Dowód:
∡CDM = ∡BAM
∡DCM = ∡ABM
∡DMC = ∡AMB
Zatem ΔDCM~ΔABM
Z podobieństwa powyższych trójkątów wynika, że MYX leżą na jednej prostej. Wystarczy pokazać,
że N należy do tej prostej. Albo inaczej, musimy pokazać, że przekątne trapezu oraz MX
przecinają się w jednym punkcie. Tutaj z pomocą przyjdzie nam twierdzenie odwrotne do tw.
Cevy. Informacje o tym możemy znaleźć w podręcznikach typowo olimpijskich. Mówi ono (to
odwrotne), że jeżeli


 .
Ale ciągle wydaje mi się, że jeżeli ΔDCM~ΔABM i MY (gdzie Y jest środkiem boku CD) przecina CD
pod kątem DYM równym AXM, to (gdzie X jest środkiem boku) to wynika, że AYM lezą na jednej
prostej. Chociaż nie wiem. Zamotałeś mnie. Ale generalnie pomysł, aby dowodzić, że K=Y wydaje
mi się najlepszy.
.
Ale ciągle wydaje mi się, że jeżeli ΔDCM~ΔABM i MY (gdzie Y jest środkiem boku CD) przecina CD
pod kątem DYM równym AXM, to (gdzie X jest środkiem boku) to wynika, że AYM lezą na jednej
prostej. Chociaż nie wiem. Zamotałeś mnie. Ale generalnie pomysł, aby dowodzić, że K=Y wydaje
mi się najlepszy.
 Jak z podobieństwa to napisz odpowiednie
równości kątów.
Jak z podobieństwa to napisz odpowiednie
równości kątów.



 Promień okręgu:R , bok kwadratu: R√2 , bok trójkata: R√3
Pole szukanego obszaru: Pole ΔOGF + pole trapezu GFPR
Pole ΔOGF
Wsp.wierzchołków kwadratu
O(0,0) , A(R√2,0} , B(R√2.R√2) , C(0,R√2)
Równania boków kwadratu
OA: y = 0 , BC: y = R√2 , OC: x = 0 , AB: x = R√2
Równania boków trójkata ODE
OD: y = tg(150)*x , OE: y = tg(750)*x
Współrzędne wierzchołków trójkata OFG
F na przecięciu prostych AB i OD
OD: y = tg(150)*x , x = R√2 , F(R√2,R√2tg(150))
G na przecięciu prostych OE i BC
OE: y = tg(750)*x , y = R√2 , G(R√2ctg(75o),R√2)
Długość odcinka OF
|OF|2 = (Fx)2 + (Fy)2
Pole trójkąta OFG
Promień okręgu:R , bok kwadratu: R√2 , bok trójkata: R√3
Pole szukanego obszaru: Pole ΔOGF + pole trapezu GFPR
Pole ΔOGF
Wsp.wierzchołków kwadratu
O(0,0) , A(R√2,0} , B(R√2.R√2) , C(0,R√2)
Równania boków kwadratu
OA: y = 0 , BC: y = R√2 , OC: x = 0 , AB: x = R√2
Równania boków trójkata ODE
OD: y = tg(150)*x , OE: y = tg(750)*x
Współrzędne wierzchołków trójkata OFG
F na przecięciu prostych AB i OD
OD: y = tg(150)*x , x = R√2 , F(R√2,R√2tg(150))
G na przecięciu prostych OE i BC
OE: y = tg(750)*x , y = R√2 , G(R√2ctg(75o),R√2)
Długość odcinka OF
|OF|2 = (Fx)2 + (Fy)2
Pole trójkąta OFG
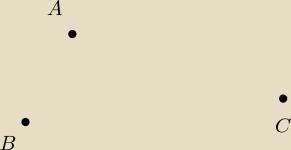 To znowu ja będę rozwiązywał zadanie. Szkoda, że taki fajniuśki temat umiera
To znowu ja będę rozwiązywał zadanie. Szkoda, że taki fajniuśki temat umiera Te trzy środki okręgów nazwijmy jako A,B,C (dla ułatwienia w taki sposób, aby |AB|≤|AC|≤|BC|).
Oznaczmy ponadto jako Ra,Rb,Rc długości promieni odpowiednio okręgów A,B,C. Oraz niech
Δl1=|AC|−|AB| i Δl2 = |BC|−|AC|. Nasze zadanie sprowadza się do wyznaczenia dł. powyższych
promieni, a to możemy zrobić rozwiązując układów równań:
Te trzy środki okręgów nazwijmy jako A,B,C (dla ułatwienia w taki sposób, aby |AB|≤|AC|≤|BC|).
Oznaczmy ponadto jako Ra,Rb,Rc długości promieni odpowiednio okręgów A,B,C. Oraz niech
Δl1=|AC|−|AB| i Δl2 = |BC|−|AC|. Nasze zadanie sprowadza się do wyznaczenia dł. powyższych
promieni, a to możemy zrobić rozwiązując układów równań:
 ΔABC: tw. cosinusów
AB2 = (b + x)2 + b2 − 2*b*(b + x)*cos(60o)
AB2 = b2 + 2*b*x + x2 + b2 − b2 − b*x
AB2 = b2 + b*x + x2
ΔDEC: tw.cosinusów
ED2 = b2 + x2 − 2*b*x*cos(120o) cos(120o) = −1/2
ED2 = b2 + x*2 + b*x
Wniosek: |AB| = |BE| q.e.d.
ΔABC: tw. cosinusów
AB2 = (b + x)2 + b2 − 2*b*(b + x)*cos(60o)
AB2 = b2 + 2*b*x + x2 + b2 − b2 − b*x
AB2 = b2 + b*x + x2
ΔDEC: tw.cosinusów
ED2 = b2 + x2 − 2*b*x*cos(120o) cos(120o) = −1/2
ED2 = b2 + x*2 + b*x
Wniosek: |AB| = |BE| q.e.d.