Macierz M.: Czy możliwe jest : 1 )Pomnożenie wektora wierszowego z wektorem kolumnowym . Jaka wyjdzie macierz? 2) Pomnożenie wektora kolumnowego z wektorem wierszowym. Jaka wyjdzie macierz? Z moich nawymyślań wynika : 1) Możliwe gdyż wewnętrzne będą takie same ( mnożna i mnożnik będą równe ) np: 1x 4 * 4x1 Powstanie macierz 1 x1 2.) Możliwe gdyż wewnętrzne będą takie same ( mnożna i mnożnik będą równe ) np: 4x1 * 1x4 Czy jest to dobrze ? Czy ktoś ma inny pomysł ?

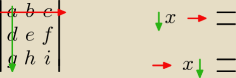
pomagacz: o taki układ chodzi?

M.: Bardziej o taki: 1) [ 1 1 3 2 ] * | 4 | 1x4 | 5 | = [18] | 1 | 1x1 | 3 | 4x1 2 ) to samo tylko owdrotnie otrzymana macierz to 4 x 4

pomagacz: no jasne, można http://pl.wikipedia.org/wiki/Mno%C5%BCenie_macierzy musi być spełniony warunek, M₁ musi mieć tyle samo kolumn co wierszy w M₂ lub na odwrót

M.: Dziękuje

pomagacz: poczekaj... po lewej zajdzie mnożenie, a po prawej nie zajdzie

M.: Hm zgadzają się wewnętrzne ( czyli 1=1) 4x1 * 1 *4 = powstała macierz bd miała wymiary 4 x 4 Ale pewnie się mylę....

Trivial: Mnożąc wektor n−wymiarowy tak jak to opisujesz, można dostać albo 'macierz' 1x1 lub nxn

Trivial: OK nie.

Trivial: Eh, jednak tak. Jakąś zaćmę miałem...

M.: Okej Czyli 2 opcja jest niemożliwa tak ? Jakiś konkretny argument ?

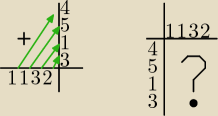
pomagacz: 1*4 + 1*5 + 3*1 + 2*3 = 4+5+3+6=18 po prawej brakuje albo trzech wierszy u góry albo trzech kolumn po lewej albo tego i tego

pomagacz: z linka powyżej: Działanie to zdefiniowane jest wyłącznie dla macierzy, z których pierwsza ma tyle kolumn, co druga wierszy. czyli pierwsza macierz jast po lewej a druga u góry, więc w drugim przypadku pierwszej macierzy brakuje trzech kolumn a drugiej trzech wierszy lub w drugiej jest o trzy elementy wiersza za dużo

M.: Dziękuje bardzo za szczegółową i wyczerpującą odpowiedź

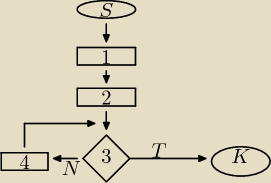
pomagacz: 1. Zapytanie −2.→ 2. wyjaśnienie −3.→ 3. Zrozumienie wyjaśnienia −T→ K. Koniec | N | v 4. Wyczerpujące wyjaśnienie −3.→