HELPP
Gox:
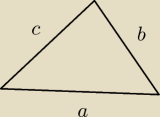
przeglądałem "Zestaw wzorów matematycznych z CKE"
| | a+b−c | |
i znalazłem wzór r= |
| |
| | 2 | |
a skąd mam wiedzięc które to ma być c? Chodzi o 2 sąsiedznie boki

| | a+c−b | |
czy mogłbo by być r= |
| |
| | 2 | |
19 sie 16:45
Vax: To działa w trójkącie prostokątnym, polecam samodzielne wyprowadzenie tego wzoru.
19 sie 16:50
Gox:
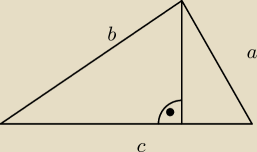
na pewno

Bo na karcie wzorów jest powyzszy rysunek.
19 sie 17:12
Vax:
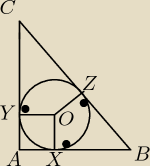
Zauważ, że AXOY jest kwadratem o boku r, XBZO oraz CYOZ deltoidami, czyli:
|AB| − r = |BX| = |BZ|
|AC| − r = |CY| = |CZ|
Dodajesz stronami:
|AB|+|AC|−2r = |BC|
2r = |AB|+|AC|−|BC|
| | |AB|+|AC|−|BC| | |
r = |
| cnd. |
| | 2 | |
19 sie 17:17
Gox: dzieki

19 sie 17:20
Gustlik: Najprościej promień okręgu wpisanego w trójkąt obliczyć tak:
gdzie:
P − pole trójkata
p − połowa obwodu trójkąta
| | 1 | |
Pole można obliczyć na kilka sposobów, np. P= |
| ah, a jeżeli jest to dowolny trókąt o |
| | 2 | |
znanych bokach, ale nieznanej wysokości, to można skorzystać ze wzoru Herona na pole:
P=
√p(p−a)(p−b)(p−c)
gdzie:
a, b, c − boki trójkata
p − połowa obwdu trójkąta, jak we wzorze na promień.
Jest jeszcze wzór na pole okręgu opisanego na trójkącie:
oznaczenia jak poprzednio: a, b, c − boki, P − pole trójkąta
19 sie 20:41
Gustlik: Mała poprwka: Jest jeszcze wzór na promień okręgu opisanego na trójkącie. Wkradł się
chochlik.
19 sie 20:43
 przeglądałem "Zestaw wzorów matematycznych z CKE"
przeglądałem "Zestaw wzorów matematycznych z CKE"


 na pewno
na pewno Bo na karcie wzorów jest powyzszy rysunek.
Bo na karcie wzorów jest powyzszy rysunek.
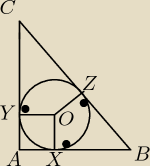 Zauważ, że AXOY jest kwadratem o boku r, XBZO oraz CYOZ deltoidami, czyli:
|AB| − r = |BX| = |BZ|
|AC| − r = |CY| = |CZ|
Dodajesz stronami:
|AB|+|AC|−2r = |BC|
2r = |AB|+|AC|−|BC|
Zauważ, że AXOY jest kwadratem o boku r, XBZO oraz CYOZ deltoidami, czyli:
|AB| − r = |BX| = |BZ|
|AC| − r = |CY| = |CZ|
Dodajesz stronami:
|AB|+|AC|−2r = |BC|
2r = |AB|+|AC|−|BC|
