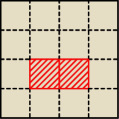
~ Trivial: Proste zadanko dla chętnych. Ile prostokątów zawiera się w kracie n×n? Na rysunku przykładowy prostokąt dla n=4.

ICSP: kwadrat to też prostokąt?

Trivial: Takie pytania od ICSP?! Tak.

Trivial: ICSP, próbujesz rozwiązać?

ICSP: spróbuje. Tylko kartkę znajdę

ICSP: buuu nie mogę policzyć ilości prostokątów przy 3 wiem ze przy pierwszym będzie 1 przy drugim będzie 9

Trivial: Nie musisz nawet tego liczyć. Zastanów się, co jednoznacznie wyznacza prostokąt w układzie współrzędnych.

ICSP: jednoznacznie

Trivial: Tak. Np. 3 punkty w przestrzeni, które nie leżą na jednej prostej jednoznacznie wyznaczą płaszczyznę.

ICSP: nadal nie wiem:( Mi to pod kombinatorykę podchodzi a z nią sobie nie radze.

Trivial: Więc dam kolejną wskazówkę: Prostokąt w układzie współrzędnych jednoznacznie wyznaczają dwa punkty (konkretnie: początek i koniec przekątnej).

Trivial: Jakie 16?

Vax:

	n2+n
Liczyłem na szybkiego, ale może jest ok (		)2 ?
	2

Trivial: Nie, ale blisko.

Jack: 48?

Jack: w8... przerobię dla n

Jack:

n 2
	*2n+n2 − też na szybko, ale zadanie ciekawe więc może się przyłożę

Trivial: Niestety nie, Jack.

Vax: Trivial jesteś pewien, że mój wzór jest zły ? Sprawdziłem dla n=1, 2, 3 i 4 i się sprawdza, więc albo źle liczę te prostokąty albo nie wiem

Jack: faktycznie, prostokąty mogą być "kobylaste" (nie w jednym rzędzie)...

Trivial: Przepraszam Vax, coś mi się pomyliło. Wzór dobry. (myślałem cały czas, że ma być z minusem, ale widzę, że mam takie samo rozwiązanie jak ty).

Jack:

	n(n+1) 2
hm a może
	4

Trivial: Nie.

Jack:

Vax: Ok, już się bałem że cały czas te prostokąty nie tak liczyłem A zadanie trzeba przyznać ciekawe

Trivial: A jakiś sposób rozwiązania? Czy sposoby aksjomatyczne (tak jest i już!)?

Vax: Szczerze mówiąc to po prostu ,,na chama" policzyłem ile jest kwadratów, potem prostokątów (2x1 , 3x1 , ... nx1) + (3x2 , 4x2 , ... , nx2) ... (n x (n−1)) i to wszystko dodałem Rozpisywać wszystko ?

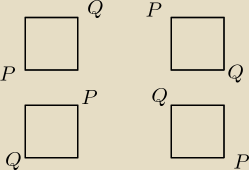
Trivial: A nie łatwiej tak: Prostokąt wyznacza para punktów (P, Q) przy czym x_P≠x_Q i y_P≠y_Q (bo wtedy otrzymujemy odcinek). Wybierając x dla pierwszego punktu mamy n+1 możliwości: {0, 1, 2, ..., n}. Wybierając y podobnie. Wybierając x dla drugiego punktu mamy już tylko n możliwości (patrz wyżej). Tak samo dla y. A więc mamy n²(n+1)² możliwości wyboru pary punktów (P, Q). Te możliwości zawierają w sobie każdy prostokąt dokładnie 4 razy (rysunek). A więc końcowa odpowiedź to:

1		n(n+1)
	n2(n+1)2 = (		)2.
4		2

Jack: podobnie wybierałem te przeciwległe wierzchołki... muszę dopracować swój wzór kombinatoryczny

Vax: Masz rację, tak jest szybciej, u mnie jest więcej babrania się z redukcją wyrazów podobnych, ale do końcowego wyniku i tak się dojdzie

Faks:

	n+1 2
czyli		2

Vax: Tak.

Trivial: Form zapisu jest dużo...

Vax: W sumie można zauważyć, że dane wyrażenie jest równe 1³+2³+...+n³, może da się pójść inną drogą, żeby z tego skorzystać

Trivial: Sposób Faksa jest chyba najłatwiejszy.

	n+1 2
Wybieramy początek i koniec boku pionowego na		możliwości i bok poziomy również na

	n+1 2		n+1 2
		możliwości, co daje		2.