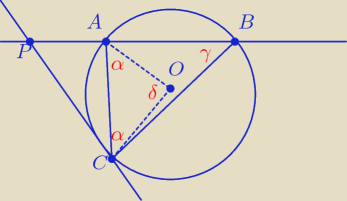
wykaż, że całek: Mógłby ktoś mi pomóc przy zadaniu: http://www.matematyka.pl/250238.htm 1. Ten punkt zrobiłbym tak: Na rysunku, który zrobiłem zaznaczyłem dane kąty. Kąt najpierw w trójkącie AOC. Są to promienie więc trójkąt jest równoramienny, dlatego δ wynosi 180^o − 2α Odnośnie kąta ACP to tam jest 90^o − α (90^o dlatego, że styczna) Już mam udowodnione, że ∡AOC = 2*∡ACP (180^o − 2α = 2 * (90^o − α)) Odnośnie udowodnienia, że ∡PBC = ∡PCA to jest to kąt środkowy, czyli dwa razy większy od kąta

	180o − 2α
wpisanego ∡PBC więc:		= 90o − α. Czyli prawdziwe jest ∡PBC = ∡PCA.
	2

Na razie dobrze?

Vax: Tak.

całek: To fajnie, ale drugiego nie wiem jak zrobić − jak się za nie wziąć. Mógłbyś dać jakąś wskazówkę?

Vax: To wynika już bezpośrednio z 1, popatrz na kąty tych trójkątów i zobacz które masz równe, żeby 2 trójkąty były podobne, wystarczy, że będą miały 2 kąty równe (z tego bezpośrednio wynika, że 3 też jest równy

całek: No to chyba są podobne (k,k,k) bo: 1. ∡PCA = ∡PBA bo mają takie same kąty mianowicie: 90^o − α A drugiego to nie wiem bo trzecie to będzie: 3. Skoro dwa kąty są takie same, to trzeci jest identyczny w drugim trójkącie

Vax: Wystarczy zauważyć, że kąt CPB jest kątem wspólnym obu trójkątów

całek: To zostało tylko 3.

	a		b
Wiem, że trzeba ułożyć równanie		= k oraz		= k ale coś nie chce mi wyjść.
	a'		b'

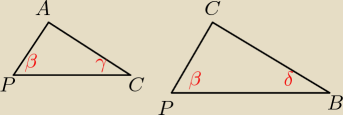
Dołączam rysunek. W trójkącie PCA, kąt γ oznacza 90^o − α. β − To jest ten wspólny kąt o którym pisałeś W trójkącie PBC β − To ten wspólny kąt o którym pisałeś δ − to ten kąt 90^o − α No i z proporcji i tak nie wychodzi Mógłbyś jakoś pomóc?

Vax: To może pokaże lewą stronę:

PC
	= ...
PA

Lewa strona to stosunek odpowiednich boków w trójkącie CPA, teraz zamień "..." na stosunek odpowiednich boków w trójkącie PCB − patrz na kąty przy jakich leżą PC i PA

całek: Dobrze wyszło już

|PC|		|PA|
	=
|PB|		|PC|

|PC|² = |PB| * |PA| Tak o ? Taka proporcja na podstawie tego rysunku ?

Vax: Dobrze

całek: To znalazłem jeszcze jedno zadanie którego w ogóle nie rozumiem: http://www.matematyka.pl/118235.htm mógłbyś jakoś pomóc, nawet nie wiem o co w nim chodzi

Vax: To wynika bezpośrednio z definicji potęgi punktu, jeżeli mamy okrąg o środku O i jakiś punkt S to zachodzi |SO|² − r² ≥ −r², prawa strona to właśnie Pot(S,O) kiedy S leży na O, w pozostałych przypadkach potęga punktu S to lewa strona.

całek: A co to jest potęga punktu? I to co napisałeś to koniec udowodnienia?

Vax: Tutaj masz wszystko opisane: http://pl.wikipedia.org/wiki/Pot%C4%99ga_punktu I po prostu, potęgą punktu S wobec okręgu o środku O jest |SO|² − r², a ponieważ |SO|² będzie zawsze nieujemne, to dane wyrażenie przyjmie najmniejszą wartość, gdy |OS|² = 0 a to zajdzie gdy S będzie leżało na O, cnd.