odległość od prostej yogi: Odległość punktu S(x,y) od prostej y = −2 wynosi 5. Oblicz współrzędne punktu S. Więc zapisałem: y + 2 = 0 A = 0 B = 1 C = 2

	|0*x + y + 2|
5 =
	1

|y + 2| = 5 y + 2 = 5 v y + 2 = −5 y = 3 v y = y = −7 I co dalej?

ICSP: takich punktów jest nieskończenie wiele. leżą na prostych y = 3 oraz y = −7 np. Punkt S(1;3), S(2;3).S(1 ; −7) , S(2 ; −7)

yogi: Dzięki, a jak rozwiązać takie zadanie: Mając podane: punkt A(−1,−2) a także punkt B(5,−2) oraz wiedząc, że odcinek AB jest podstawą trójkąta równoramiennego. Oblicz punkt C wiedząc, iż promień okręgu opisanego na trójkącie ABC wynosi 5. W odpowiedziach mam aż 4 wyniki podane, jak oni to zrobili?

ICSP: C(2 ; −11) C(−2;7)

yogi: (2, −11) lub (2,−3) lub (2, − 1) lub (2,7)

yogi: A jak wyszły Tobie przedtem te dwa wyniki? Bo dobre są. Obliczyłeś już? Czy znalazłeś gdzieś?

ICSP: nie wiem jakim cudem im wyszło (2;−3) oraz (2; −1). Myślę że błąd w odpowiedziach. Poczekam jeszcze na wypowiedź innych.

ICSP: Tak na szybko z wykorzystaniem trójkątów egipskich policzyłem.

ICSP: a nie już wszystko mi wyszło Zapomniałem o jednym bardzo istotnym fakcie

ICSP: zaraz napiszę bo do tego będzie trzeba jeszcze rysunek.

yogi: Ja zacząłem robić swoim sposobem. Mianowicie: punkty A i B są podane, więc są one na okręgu. Promień mam podany to mam: (x−a)² + (y − b)² = 25 gdzie S = (a, b)

⎧	(−1 − a)2 + (−2 − b)2 = 25
⎩	(5−a)2 + (−2 − b)2 = 25

Rozwiąże ten układ równań i otrzymam postać kanoniczną okręgu. Następnie obliczę prostą prostopadłą do prostej AB przechodzą przez jej środek punkt D. Punkt C będzie miał postać C(x, ax + b) I podstawie w równaniu okręgu ax + b za y i powinno wyjść Co o tym sądzisz?

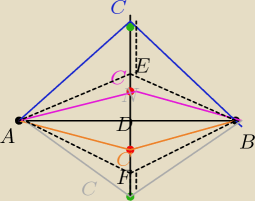
ICSP: najpierw ustalamy że długość odcinka |AB| = 6 masz na rysunku 4 trójkąty. Będziemy je oznaczać w zależności od długości koloru ich ramion. Najpierw bardzo ważne jest aby zauważyć że |CC| = |CC| = 10 Odcinki przerywane to promienie. Analiza: |AD| = 3 |AF| = 5 ⇔ |DF| = 4(własności trójkąta Pitagorajskiego, egipskiego. Jak ich nie znasz licz z pitagorasa. Odcinek |CF| = |EC| = 5(promień) |DF| + |CF| = 9 (jak i w dół tak i w górę. Punkt D ma współrzędne (2; −2) tak więc pierwsze dwa punkty będą miały współrzędne C(2 ; −2±9) Zostały jeszcze do wyznaczenia dwa punkty: |ED| = 4 |EC| = 5 (promień) dlatego |DC| = 1 Ostatnie dwa punkty mają współrzędne C(2 ; −2±1)

yogi:

⎧	(−1 − a)2 + (−2 − b)2 = 25
⎩	(5−a)2 + (−2 − b)2 = 25

1^o. (−1 − a)² + (−2 − b)² = 25 1 + 2a + a² + 4 + 4b + b² = 25 2^o. (5 − a)² + (−2 − b)² = 25 25 − 10a + a² + 4 + 4b + b² = 25 Podstawiając: 1 + 2a + a² + 4 + 4b + b² = 25 − 10a + a² + 4 + 4b + b² 1 + 2a + a² = 25 − 10a + a² −12a = 24 / : (−12) a = −2 Dobrze to na razie?

ICSP: idąc twoim sposobem: A(−1;−2) B(5;−2) r = 5. Układ równań: (−1−a)² + (−2−b)² = 25 (5−a)² + (−2−b)² = 25 Metoda rozwiązywania układów równań zwana metodą zgadywania( raczej nie uznają na maturze, nie wiem czemu) a = 2, b = 2 a = 2 b = −6 Czyli mamy okrąg: (x−2)² + (y−2)² = 25 (x−2)² + (y+6)² = 25 Teraz zauważamy że prosta AB jest równoległa do osi OX tak więc prosta prostopadła do niej będzie miała równanie x = c gdzie c jest współrzędną x środka odcinka: 2. Wstawiamy dwójkę do tych dwóch równań i odczytujemy rozwiązanie: (y − 2)² = 25 ⇔ y = −3 v y = 7 (y+6)² = 25 ⇔ y = −1 v y = −11 i zapisujesz te punkty: C(2;−11) C(2;−3) C(2;−1) C(2;7)

yogi: Czyli dobrze myślałem, tylko możesz pomóc rozwiązać ten układ ?

ICSP: przecież ci rozwiązałem

Eta: dla ICSP

yogi: Ale krok po kroku:

⎧	(−1 − a)2 + (−2 − b)2 = 25
⎩	(5−a)2 + (−2 − b)2 = 25

Bo mi coś nie wychodzi

ICSP: (a+1)² + (b+2)² = 25 (5−a)² + (b+2)² = 25 (a+1)² = 25 − (b+2)² (5−a)² = [Z{25 − (b+2)²]] (a+1)² = (5−a)² ⇔ (a+1)² − (5−a)² = 0 ⇔ (a+1 −5 + a)(a+1 + 5 − a) = 0 ⇔ (2a − 4)6 = 0 ⇔ 2a − 4 = 0 v 6 = 0 drugie oczywiście sprzeczne 2a −4 = 0 ⇔ a = 2 (a+1)² = 25 − (b+2)² ⇔ 9 = 25 − (b+2)² ⇔ (b+2)² = 16 ⇔ (b+2)² − 4² = 0 ⇔ (b+2−4)(b+2+4) = 0 ⇔ b = 2 v b = −6

ICSP: buuu nie wyszło mi drugie zielone:(

yogi: A tak jak ja rozwiązywałem to nie można? Że cały czas wzory skróconego mnożenia a na koncu tylko podstawiamy?

Eta: (5−a)²=25−(b+2)² Teraz wyszło "drugie zielone"

Eta: @ yogi porównaj równania stronami, otrzymasz: (a+1)²=(5−a)² .......... (tak jak podał Ci ICSP

ICSP: yogi oczywiście ze można. Jeżeli chcesz sobie dodawać obliczeń i przez to zwiększać prawdopodobieństwo pomyłki. No i oczywiście tracisz czas.

Eta: A może yogi.............chce "jechać z Gdańska do Sopotu przez Londyn" ?

ICSP: skoro lubi

Eta:

yogi:

⎧	(a + 1)2 + (b + 2)2 = 25
⎩	(5−a)2 + (b + 2)2 = 25

1^o. a² + 2a + 1 + b² + 4b + 4 = 25 2^o 25 − 10a + a² + b² + 4b + 4 = 25 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

⎧	a2 + 2a + 1 + b2 + 4b + 4 = 25
⎩	25 − 10a + a2 + b2 + 4b + 4 = 25

a² + 2a + 1 = 25 − 10a + a² 2a + 1 = 25 − 10a 12a = 24 / : 12 a = 2 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

⎧	(2)2 + 2*2 + 1 + b2 + 4b + 4 = 25
⎩	25 − 10*2 + (2)2 + b2 + 4b + 4 = 25

⎧	4 + 4 + 1 + b2 + 4b + 4 = 25
⎩	25 − 20 + 4 + b2 + 4b + 4 = 25

⎧	b2 + 4b + 13 = 25
⎩	b2 + 4b + 13 = 25

b² + 4b + 13 = 25 b² + 4b − 12 = 0 Δ = 16 + 48 = 64 ⇒ √Δ = 8

	−4 − 8
b1 =		= −6
	2

	−4 + 8
b2 =		= 2
	2

Dziękuje za pomoc

yogi: Jeszcze do tego zadania mam taki podpunkt:

	9
b) Wykaż, że gdyby wpisać w ten trójką równoramienny okrąg to promień jest mniejszy od
	4

Bardzo proszę o pomoc

ICSP: ja tam widzę 2 różne trójkąty równoramienne.