wektory deria: Grający w golfa uderzył piłkę 3 razy zanim wpadła na dołka znajdującego się na trawniku. Najpierw piłka poleciała 12m na północ, potem 6m na południowy wschód i w końcu 3m na południowy zachód. Obliczyć jakie musiałoby być przemieszczenie, żeby piłka wpadła do dołka za pierwszym razem. Proszę o pomoc.

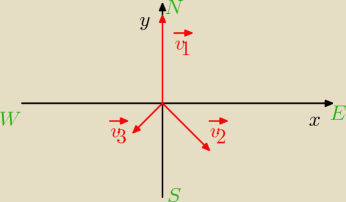
Trivial: Przyjmijmy konwencję jak na rysunku. Niech wektory v₁, v₂, v₃ oznaczają kolejne wektory przemieszczenia piłki na płaszczyźnie pola golfowego, a wektor v będzie ich sumą wektorową. v₁ − 12 m na północ, czyli v₁ = (0, 12) v₂ − 6 m na południowy wschód, czyli v₂ = (a, −a), a>0 i ||v₂|| = 6. ||v₂|| = √a²+(−a)² = a√2 = 6 → a = 3√2 v₂ = (3√2, −3√2) v₃ − 3 m na południowy zachód, czyli v₃ = (−b, −b), b>0 i ||v₃|| = 3. ||v₃|| = √(−b)² + (−b)² = b√2 = 3 → b = ³₂√2. v₃ = (−³₂√2, −³₂√2) v = v₁ + v₂ + v₃ = (0+3√2−³₂√2, 12−3√2−³₂√2) =

	3√2		9√2
= (		, 12−		).
	2		2

deria: dzieki