Prawdopodobienstwo
mac: W urnie jest 5 kul białych i 4 kule czarne. Z tej urny wyjmujemy losowo dwie kule. Oblicz, ile
kul białych należy dołożyć do tej urny, aby prawdopodobieństwo wyrzucenia co najmniej jednej
kuli białej było większe od 7/8.
10 sie 01:27
mac: a i odpowiedz to co najmniej 2 kule

10 sie 01:27
Gustlik: W urnie jest 5 kul białych i 4 kule czarne. Z tej urny wyjmujemy losowo dwie kule. Oblicz, ile
kul białych należy dołożyć do tej urny, aby prawdopodobieństwo wyrzucenia co najmniej jednej
kuli białej było większe od 7/8.
n − ilość dołożonych kul białych
5+n − ilość kul białych po dołożeniu
4 − ilość kul czarnych
5+n+4=9+n − łączna ilość kul po dołozeniu
| | (n+9)! | | (n+9)! | |
|Ω|=C9+n2= |
| = |
| =
|
| | 2!*(n+9−2)! | | 2(n+7)! | |
| | (n+7)!(n+8)(n+9) | | (n+8)(n+9) | |
= |
| = |
|
|
| | 2(n+7)! | | 2 | |
Liczę prawdopodobieństwo zdarzenia A' − dopełnienia A:
A' − nie wylosowano kuli białej (czyli wylosowano 2 czarne)
| | 4! | | 2!*3*4 | |
|A'|=C42= |
| = |
| =3*2=6
|
| | 2!*2! | | 2!*1*2 | |
Liczę "właściwe" zdarzenie:
|A|=|Ω|−|A'|
| | (n+8)(n+9) | | (n+8)(n+9)−12 | |
|A|= |
| −6= |
| =
|
| | 2 | | 2 | |
| | n2+9n+8n+72−12 | | n2+17n+60 | |
= |
| = |
|
|
| | 2 | | 2 | |
| | n2+17n+60 | | (n+8)(n+9) | |
P(A)= |
| / |
| =
|
| | 2 | | 2 | |
Rozwiąż teraz nierówność wymierną − wskazówka:
https://matematykaszkolna.pl/strona/2536.html − tu masz podobny przykład.
| n2+17n+60 | | 7 | |
| > |
|
|
| (n+8)(n+9) | | 8 | |
I ze zbioru rozwiązań wypisz liczby € N
+.
12 sie 00:23
Trivial:
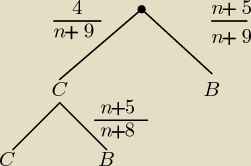
Proponuję rozwiązanie krzakoterapią, w tym przykładzie wydaje się prostsze.
Interesuje nas prawdopodobieństwo wyboru przynajmniej jednej kuli białej. Możemy wybrać
najpierw czarną, a potem białą lub białą, a następnie kulę dowolnego koloru.
Oznaczamy:
n−liczba białych kul, którą trzeba dołożyć, wtedy jest 4 kule czarne i n+5 kul białych.
Wszystkich kul jest n+9. Z drzewka odczytujemy:
| | 4 | | n+5 | | n+5 | | 7 | |
P(A) = |
| * |
| + |
| > |
| |
| | n+9 | | n+8 | | n+9 | | 8 | |
Po rozwiązaniu tej nierówności dojdziesz do postaci:
Czyli trzeba dołożyć przynajmniej dwie.
12 sie 10:37

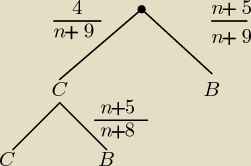 Proponuję rozwiązanie krzakoterapią, w tym przykładzie wydaje się prostsze.
Interesuje nas prawdopodobieństwo wyboru przynajmniej jednej kuli białej. Możemy wybrać
najpierw czarną, a potem białą lub białą, a następnie kulę dowolnego koloru.
Oznaczamy:
n−liczba białych kul, którą trzeba dołożyć, wtedy jest 4 kule czarne i n+5 kul białych.
Wszystkich kul jest n+9. Z drzewka odczytujemy:
Proponuję rozwiązanie krzakoterapią, w tym przykładzie wydaje się prostsze.
Interesuje nas prawdopodobieństwo wyboru przynajmniej jednej kuli białej. Możemy wybrać
najpierw czarną, a potem białą lub białą, a następnie kulę dowolnego koloru.
Oznaczamy:
n−liczba białych kul, którą trzeba dołożyć, wtedy jest 4 kule czarne i n+5 kul białych.
Wszystkich kul jest n+9. Z drzewka odczytujemy: