[C[zadanie dla chętnych]] b.: f : R −> R jest różniczkowalna i ma pochodną rosnącą, uzasadnić, że funkcja g : R−>R określona wzorami

	f(x)−f(0)
g(x) =		, dla x≠0,
	x

oraz g(0)=0, jest rosnąca

b.: podbijam

Godzio: To dla pewności, pochodna rosnąca oznacza że funkcja f jest funkcją rosnącą tak ?

Godzio: Moim zdaniem, funkcja g(x) jest rosnąca w przedziale (0,∞)

Trivial: Weźmy np. f(x) = x² + x, wtedy: f'(x) = 2x + 1 − rosnąca

	⎧	x + 1, dla x≠0
g(x) =	⎨
	⎩	0, dla x=0

Funkcja g nie jest rosnąca.

b.: przepraszam pomyłka: powinno być g(0)=f '(0) (pochodna f w zerze)

b.: pochodna rosnąca (na jakimś przedziale) oznacza, że funkcja jest wypukła (na tym przedziale) pochodna dodatnia (na jakimś przedziale) oznacza, że funkcja jest rosnąca (na tym przedziale)

b.: podbijam. wskazówka: tw. Lagrange'a

Basia: Witaj b. To łatwe zadanko, tylko żeby się nim w ogóle zainteresować trzeba zajmować się matematyką, nie mechanicznymi rachunkami. Szkoła tego nie uczy. Studia inne niż sama matematyka niestety też nie. Stąd jak sądzę brak odzewu. Pozdrawiam

Basia: O przepraszam, Trivial się zainteresował, nie studiuje matematyki, ale za to studiuje na AGH. Tam na innych kierunkach też uczą matematyki, nie tylko rachowania. Trivial do dzieła ! Dasz sobie radę !

Trivial: 1. Sprawdźmy, czy g jest ciągła. Wiemy, że f jest różniczkowalna na R a więc:

	f(x)−f(0)
limx→0 g(x) = limx→0		=[H]= limx→0 f'(x) = f'(0).
	x

Zatem g jest ciągła na R. 2. Z twierdzenia Lagrange'a wiemy, że jeżeli funkcja f jest różniczkowalna na (a, b), to:

f(b)−f(a)
	= f'(c), dla pewnego c∊(a, b).
b−a

Czyli, gdy x>0:

f(x)−f(0)
	= f'(c) dla c∊(0, x)
x

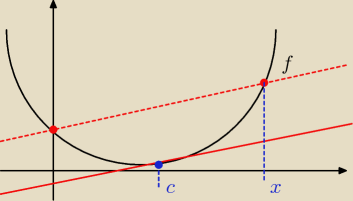
Skoro wiemy, że f'(x) jest rosnąca, czyli f(x) jest wypukła, to z interpretacji geometrycznej widzmy, że wraz ze wzrostem x będzie rosło również c. gdy x<0:

f(x)−f(0)		f(0)−f(x)
	=		= f'(c), dla c∊(x, 0)
x		|x|

Analogicznie: wraz ze spadkiem x będzie maleć c. 3. A zatem g(x) = f'(c), przy czym c rośnie wraz z x, ale f'(x) jest również rosnąca, czyli g(x) jest rosnąca.

b.: Zgadza się Można też uniknąć powoływania się na rysunek: g jest, jak sprawdziłeś, ciągła, poza zerem jest też różniczkowalna i jej pochodna wynosi

	f'(x)x − f(x)
g'(x) =		,
	x2

żeby pokazać, że jest dodatnia, wystarczy pokazać, że f'(x)x > f(x), czyli dla x>0

	f(x)
f'(x) >		= f'(c) dla pewnego c ∊ (0,x)
	x

To jest prawda, bo f' jest rosnąca. Zatem dla x>0 mamy g'(x)>0. Dla x<0 można podobnie pokazać, że g'(x)>0. Stąd g jest rosnąca. (Pytanie: Dlaczego nie musimy się przejmować różniczkowalnością g w zerze?)

Trivial: Bo dla x=0: g(x) = f'(0)?

b.: np. f(x)=x² dla x<0, i f(x)=2x² dla x≥0 spełnia warunki zadania, wówczas g(x) = x dla x<0, g(x)=2x dla x≥0, czyli g nie jest różniczkowalna w zerze

PIDAR: