 W(x) = (x+a)(x+2a)(x+3a)(x+4a).
Problem: Liczba rozwiązań równania W(x) = 4a4.
Analizę problemu rozbijamy na przypadki:
1. Niech a = 0, wtedy:
x4 = 0 → jedno rozwiązanie.
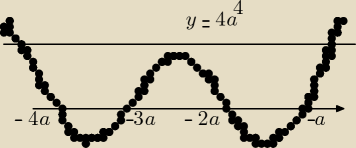
2. Niech a > 0, wtedy rozwiążemy problem rysując wykres wielomianu.
Zauważamy, że nasz wielomian jest w przedziale (−3a, −2a) niezwykle symetryczny i zgadujemy,
że największą lokalną wartość przyjmuje dla x=−2.5a (jeżeli znasz pochodne możesz sobie to
sprawdzić, ale symetria jest wystarczającym powodem
W(x) = (x+a)(x+2a)(x+3a)(x+4a).
Problem: Liczba rozwiązań równania W(x) = 4a4.
Analizę problemu rozbijamy na przypadki:
1. Niech a = 0, wtedy:
x4 = 0 → jedno rozwiązanie.
2. Niech a > 0, wtedy rozwiążemy problem rysując wykres wielomianu.
Zauważamy, że nasz wielomian jest w przedziale (−3a, −2a) niezwykle symetryczny i zgadujemy,
że największą lokalną wartość przyjmuje dla x=−2.5a (jeżeli znasz pochodne możesz sobie to
sprawdzić, ale symetria jest wystarczającym powodem  ).
W(−2.5a) = (−1.5a)*(−0.5a)(0.5a)(1.5a) = 0.5625a4.
Ta wartość jest mniejsza niż 4a4, czyli część środkowa nigdy nie zwiększa liczby rozwiązań
równania. Mamy więc dla każdego a > 0 dwa rozwiązania.
3. Niech a < 0, wtedy poprzez analogię do punktu 2 wnioskujemy, że mamy dwa rozwiązania.
Ostatecznie równanie ma:
).
W(−2.5a) = (−1.5a)*(−0.5a)(0.5a)(1.5a) = 0.5625a4.
Ta wartość jest mniejsza niż 4a4, czyli część środkowa nigdy nie zwiększa liczby rozwiązań
równania. Mamy więc dla każdego a > 0 dwa rozwiązania.
3. Niech a < 0, wtedy poprzez analogię do punktu 2 wnioskujemy, że mamy dwa rozwiązania.
Ostatecznie równanie ma:
| ⎧ | 1 rozwiązanie rzeczywiste, gdy a=0 | |
| ⎩ | 2 rozwiązania rzeczywiste, gdy a∊R\{0} | . |
| x | x | x | x | |||||
( | + 1)( | + 2)( | + 3)( | + 4) = 4 | ||||
| a | a | a | a |
| x | |
= u i otrzymujemy: | |
| a |
| 5 | ||
u + | = y | |
| 2 |
| 3 | 1 | 1 | 3 | |||||
(y − | )(y − | )(y + | )(y + | ) = 4 | ||||
| 2 | 2 | 2 | 2 |
| 1 | 9 | |||
(y2 − | )(y2 − | ) = 4 | ||
| 4 | 4 |
| 5 | ||
y2 − | = z | |
| 4 |
| 5 | ||
y2 = | + √5 | |
| 4 |
| 5 | ||
y2 = | − √5 < 0, to odrzucamy | |
| 4 |
| 5 | 5 | |||
u = − | + √5/4 + √5 lub u = − | − √5/4 + √5 | ||
| 2 | 2 |
| 5 | 5 | |||
x = a(− | + √5/4 + √5) lub x = a(− | − √5/4 + √5) | ||
| 2 | 2 |
