znajdź równania stycznych Ewa: Znajdź równania stycznych do okręgu x2+y2=1 przechodzących przez punkt P=(0,2)

Godzio: Styczne mają równania: y = ax + 2 ⇒ ax − y + 2 = 0 x² + y² = 1 ⇒ S(0,0) r = 1 Odległość środka okręgu od stycznych jest równa długości promienia:

	2
d = r ⇒		= 1 ⇒ 2 = √a2 + 1 ⇒ a2 = 3 ⇒ a = √3 lub a = −√3
	√a2 + 1

Odp: 1 styczna: y = √3x + 2 2 styczna: y = −√3 + 2

ICSP: Witaj Godziu

Godzio: Witam

Ewa: A jak napisać równania prostych przechodzących przez p A o śr w p.(2,−2) i r=3 a)(5,−2) b)(5,5) próbowałam zrobić adekwatnie do tego, ale coś mi nie idzie

Godzio: Rozumiem tak: środek okręgu S(2,−2) promień r = 3, punkt A(5, − 2) tak ?

Ewa: tak

Godzio: W pierwszym trzeba zauważyć że punkt A spełnia równanie okręgu, (x − 2)² + (y + 2)² = 9 po podstawieniu: (5 − 2)² + (−2 + 2)² = 9 9 = 9 Czyli tutaj jest jedna styczna: x = −2 (ponieważ jedna ze współrzędnych punktu A jest taka sama jak współrzędna środka ) b) Tutaj podobnie, tyle że prosta będzie postaci y = ax + b (5,5) ⇒ y = ax + b ⇒ 5 = 5a + b ⇒ b = − 5a + 5 y = ax − 5a + 5 ⇒ ax − y − 5a + 5 = 0 S(2,−2) r = 3

	|2a + 2 − 5a + 5|
d =		= 3 ⇒ |−3a + 7| = 3√a2 + 1 /2 ⇒
	√a2 + 1

9a² − 42a + 49 = 9a² + 9 − 42a = − 40

	20
a =
	21

	20		5
y =		x +		/ * 21 ⇒ 20x − 21y + 5 = 0
	21		21

Ewa: ale godzio zauważ, że w b) są dwie styczne, jedna jest o takim równaniu, jakie wyliczyłeś, a druga to x=5, ale nie wiem jak do tego dojść. Tak wywnioskowałam z rysunku, który sobie sporządziłam w układzie współrzędnych

Godzio: No tak ... Takie rozwiązanie nie pokaże nam stycznej postaci x = c

Ewa: A wiesz jak do tego dojśc?

Godzio: Tych prostych chyba nie da się wyznaczyć po przez obliczenie

Jack: tutaj było podobne zadania, zerknij: https://matematykaszkolna.pl/forum/99333.html

Basia: ad. b błąd polega na założeniu , że prosta ma równanie y=ax+b to założenie jest niczym nie uzasadnione, bo nie każda prosta ma równanie tej postaci dlatego w zadaniach tego typu powinno się korzystać z równania: Ax+By+C=0 co jednak komplikuje obliczenia, albo, co jest prostsze, rozważać zawsze dwa przypadki: 1. prosta ma równanie y=ax+b 2. prosta ma równanie x=c

Ewa: Basiu, a co myślisz o obliczeniu punktów styczności, a następnie na ich podstawie obliczenie dwóch prostych AB i AC. I tym sposobem wyszła mi prosta x=5, ale znów ta druga styczna mi wyszła jakaś dzika. Wolałabym rozkmnić zadanie z ta postacią ogólna, no ale cięzko niestety.

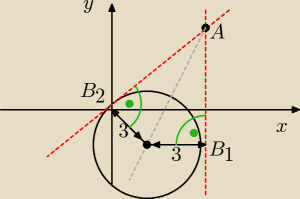
Jack: b) 1. Żeby wyznaczyć prostą styczną do okręgu S(2,−2) i r=3 przechodzącą przez A(5,5), musimy znaleźć punkt na okręgu (x−2)²+(y+2)²=9 ⇒ y= √9−(x−2)²−2 ∨ y= −√9−(x−2)²−2 2. Łatwo policzyć, że odległość A od B jest równa 7 (ponieważ odl. A od O jest równa √(5−2)²+(5+2)²=√58, a promień okręgu 3). 3.a Układamy równanie na odległość A(5,5) od B(x,√9−(x−2)²−2), która jest równa 7. (x−5)²+(√9−(x−2)²−2−5)²=49 x²−10x+25+9−(x−2)²−14√9−(x−2)²=0 x²−10x+25+9−x²+4x−4=14√9−(x−2)² −6x+30=14√9−(x−2)² /² (zał. x≤5) 36(x−5)²=196(−x²+4x+5) 36(x−5)²=196(x+1)(x−5) (x−5)[36(x−5)−196(x+1)]=0 (x−5)(36x−180−196x+196)=0 (x−5)(−160x+16)=0

	1
−160(x−5)(x−		)=0
	10

x=5 ∨ x=0,1 ∊D 3.b Można jeszcze sprawdzić rozwiązania dla dolnego okręgu, ale widać, że będzie brak rozwiązań, więc pominę. 4. Dla x₁=5 mamy z równania okręgu (x−2)²+(y+2)²=9 , że y₁=−2, stąd B(5,−2), stąd wobec A(5,5) prostą jest linia pionowa x=5

	1
Dla x2=		mamy z y= √9−(x−2)2−2, że y2=√5,39−2 (pewnie gdzieś się machnąłem).
	10

Stąd mając dwa punkty również można będzie wyznaczyć prostą. Metoda jest dokładnie analogiczna do tej, którą podałem w linku...

Basia: Nie bardzo rozumiem jakim sposobem najpierw wyznaczyłaś punkty styczności ? Przecież tak długo, jak długo nie wiemy o jaką prostą chodzi nie wiemy też o jaki punkt styczności chodzi. Odradzam użeranie się z postacią ogólną. Po pierwsze dlatego, że są tam trzy parametry i trudno z nimi walczyć. Po drugie dlatego, że ostatecznie i tak trzeba rozważyć dwa przypadki:

	A
B≠0 co się sprowadza do równania w postaci kierunkowej y =		x+Y{C}{B}
	B

	C
B=0 co się sprowadza do równania x=
	A

Ostatecznie najbardziej efektywne (nie biorąc pod uwagę metody obrazkowej) jest rozważenie tych dwóch przypadków y=ax+b i x=c. Można zresztą szybko sprawdzić czy ten drugi ma prawo zachodzić, bo zachodzi ⇔ x_s+r = x₀ lub x_s−r=x₀ gdzie x_s odcięta środka, a x₀ odcięta punktu przez który ma przejść styczna.

Jack: przy drugim pierwiastku się pomyliłem... nie będzie x₂=0,1. No ale to już rachunki, a muszę uciekać... Liczę, że ktoś mnie poprawi

Basia: Jack oczywiście metoda dwusiecznej jest poprawna tylko po co to aż tak komplikować ? Nie prościej zbadać kiedy każdy z dwóch układów równań z parametrem ma dokładnie jedno rozwiązanie? Jeden to ten, który rozwiązał Godzio Drugi to: (x−2)²+(y+2)²=9 x = c

Jack: to chyba nie taka straszna komplikacja... Poza tym od razu mamy wszystkie rozwiązania, nie musimy się domyślać, że jest jeszcze jakieś rozwiązanie, którego inna metoda nie pozwoliła znaleźć. Gdybyśmy wiedzieli ile i jakiego rodzaju mamy rozwiązania, to... może było by nieco prościej (rachunkowo). Nie upieram się, niemniej w "metodzie dwusiecznej" (daję cudzysłów bo metodą dwusiecznej można by też nazwać metodę bazującą na tangensach) mamy tak naprawdę jedno równanie z którego wychodzą wszystkie rozwiązania.

Basia: ależ wiemy, jeżeli chwilę pomyślimy przez każdy punkt płaszczyzny leżący na zewnątrz okręgu przechodzą [P[dwie proste styczne]] do tego okręgu 1. pierwszy sposób rozumowania skoro rozwiązanie układu równanie okręgu + prosta y = ax+b dało tylko jedną prostą, to druga musi mieć równanie y = c 2. drugi sposób rozumowania jeżeli x_s+r = x₀ lub x_s−r=x₀ to jedną ze stycznych musi być prosta x=x₀ drugą dostaniemy rozwiązując układ jak wyżej

Jack: Ok, faktycznie dużo krócej, a i rozumowanie lekkie