trygonometria pomozecie: oblicz pole S trojkata rozwartokatnego ABC, majac dane: IABI=c, kat CAB=α, (α>90), kat ABC=β. odp.S=c2/2(ctgβ−ctg(180−α))

Godzio: γ = 180 − α − β, sinγ = sin(180 − (α + β) ) = sin(α + β) Z twierdzenia sinusów:

c		a		sinα		sinα
	=		⇒ a = c *		⇒ a = c *
sinγ		sinα		sinγ		sin(α + β)

	1		1		sinα
S =		a * c * sinβ =		c *		* c * sinβ =
	2		2		sin(α + β)

	c2sinαsinβ
=
	2sin(α + β)

Jak chcesz to możesz się pobawić w przekształcenie tego wyrażenia i dojść do Twojej odpowiedzi, ale to jest równoznaczne więc chyba nie trzeba

pomozecie: a mozna innym sposobem?

ICSP: Oczywiście że można inaczej. Jednakże Godzio pokazał ci najprostszy sposób. Chyba że jesteś z podstawy.

pomozecie: a moglbym prosic o inny.

ICSP: Godzio zaraz ci to rozwiąże innym. Ja nie mogę gdyż nie chce wprowadzać w błąd. Wczoraj wielką gafę walnąłem i teraz straciłem wiarę we własne możliwości.

Trivial: ICSP, który to temat? Nie czytałem naprawdę...

ICSP: https://matematykaszkolna.pl/forum/99313.html

Trivial: erm, no bez przesady.

ICSP: powiedz mi jak można dzielić przez 0

Trivial: Można. Jak już powiedziałem, autor mojej książki od fizyki nie ma takich problemów. Dla niego

	a
		= ∞.
	0

ICSP: przecież nie jestem autorem twojej książki do matematyki jak dla mnie powinniśmy w rozwiązywaniu zadań opierać się na faktach a nie na przemyśleniach twojego autora książki od fizyki

Trivial: Pytałeś się jak można dzielić przez 0 to ci powiedziałem.

ICSP: no dobrze już dobrze. Jednak ktoś na moim poziomie nie powinien popełniać takich błędów.

Trivial: Czy ja wiem... Ja zazwyczaj popełniam proste błędy tego typu.

ICSP: To dlaczego nawet z rysunku odczytałem błędnie?

Basia: Trivial to nie jest dzielenie przez 0, tylko uproszczony zapis granicy ułamka; dosyć często stosowany i tak samo niezupełnie poprawny jak zapis (chyba w każdym języku programowania) i = i+1 lub, z większą dbałością o logikę, i:=i+1

ICSP: Oż ty. Chciałeś mnie oszukać

Trivial: Tak, wiem, że autorowi chodzi o zapis graniczny, ale mimo tego dziwnie wygląda. W programowaniu nie ma problemu, tam = nie oznacza = matematycznego.

Trivial: ICSP chciałem cię oszukać, muahaha!!1

ICSP: :(

1: = oznacza także "równa się"; przykłady: if x=2 goto :ET1 while x=2 do ..... enddo a w tym zapisie i = i+1 oznacza "podstaw...." , "zwiększ o jeden" i jest to pewna niekonsekwencja dlatego niektóre języki stosują jednak zapis i:=i+1

Basia: Ki diabeł ? To wyżej to ja..........

ICSP: Basia od kiedy jesteś 1?

Basia: Nie wiem

Trivial: Zależy wszystko od języka. W tym przykładzie rozróżnia się wyrażenia logiczne od przypisań (nie jest to trudne). Ale np. w języku C do porównań używa się ==, a do przypisań =.

Basia: Tak samo, jak nie jest trudne rozróżnienie kiedy mowa o zwykłym dzieleniu, a kiedy o granicach.

Trivial:

pomozecie: a moze mozna wyliczyc h?

ICSP: tak. Właśnie na tym polega druga metoda. Jednakże jak widzisz Godzia nie ma i dlatego Trivial zgłosił się na ochotnika.

Trivial: Myślę, że ICSP musi zadośćuczynić i wybaczyć sobie −> zrobienie tego zadania na pewno mu pomoże.

Godzio:

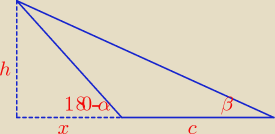
	x
ctg(180 − α) =		⇒ x = htg(180 − α)
	h

	x + c
ctgβ =		⇒ x + c = h * ctgβ ⇒ hctg(180 − α) + c = h * ctgβ ⇒
	h

c = h(ctgβ − ctg(180 − α))

	c
h =
	ctgβ − ctg(180 − α)

	c * h		c2
P =		=
	2		2(ctgβ − ctg(180 − α))

Bogdan: Można rozwiązać zadanie i tak: γ = 180^o − (α + β) ⇒ sinγ = sin(α + β)

	c		c
Z tw. sinusów: 2R =		⇒ R =
	sinγ		2sin(α + β)

	c2*sinα*sinβ		c2
Pole trójkąta P=2R2*sinα*sinβ*sinβ = 2*		=
	4sin2(α + β)		2(ctgβ − tgα)

	sinα*sinβ		1
Przejście od		do		pozostawiam do samodzielnego
	sin2(α + β)		ctgβ − tgα

przekształcenia