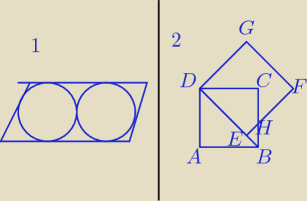
Zadania na wykazywanie daruś: Pomożecie przy takich zadaniach:? 1. Mając dany równoległobok wpisano w niego dwa takie same okręgi (styczne zewnętrznie). Uzasadnij, iż średnice tych okręgów są równe różnicy długości dłuższego i krótszego boku równoległoboku. 2. Mając kwadrat DEFG który jest takich samych rozmiarów jak kwadrat ABCD oraz wiedząc, że odcinek DE leży na odcinku DB i bok kwadratu EF przecina się z bokiem BC w punkcie H. Uzasadnij, że

|HB|
	= √2
|HC|

Bardzo proszę o pomoc

Basia: niech a oznacza długość boku kwadratów BD = a√2 EB = a√2 − a = a(√2−1) ∡BEH = 90 ∡HBE = ∡BHE = 45

	EB
sin45 =
	HB

√2		a(√2−1)
	=
2		HB

	2a(√2−1)		2√2a(√2−1)
HB =		=		= √2a(√2−1)
	√2		2

HC = a−HB HC = a − √2a(√2−1) = a[ 1 − √2(√2−1) ] = a(1−2+√2) = a(√2−1)

HB		√2a(√2−1
	=		= √2
HC		a(√2−1)

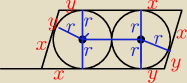Basia: x+2r+y = a x+y = b 2r = a − (x+y) = a−b