wielomiany iga: Bardzo proszę o pomoc, gdyż nie mam żadnego pomysłu. Wielomian W(x) = x²⁰¹¹ −x +1 : A. ma co najmniej 1 pierwiastek rzeczywisty, B. ma co najwyżej 1 pierwiastek rzeczywisty, C. ma pierwiastek wymierny, D. przy dzieleniu przez x daje resztę 1. Poprawne mają być odpowiedzi: A, B i D. Ale nie wiem dlaczego. Proszę o pomoc.

ICSP: A i B wynika z definicji. D:

x2011 − x + 1		1
	= x2010 − 1 +		. To co zostało w liczniku ułamka jest resztą.
x		x

iga: Proszę, napisz, dlaczego A i B wynika z definicji, bo nie rozumiem.

ICSP: Każdy wielomian nieparzystego stopnia posiada co najmniej jeden pierwiastek rzeczywisty lub o parzystą liczbę więcej. Przy czym może posiadać maksymalnie tyle pierwiastków ile wynosi jego stopień.

iga: Przepraszam Cię ICSP: , ale gdzie można znaleźć to pierwsze zdanie, bo nie słyszałam o takim twierdzeniu. Skąd to się wzięło? Wybacz.

ICSP: Znam to twierdzenie od trzech lat ale nigdy nie potrafiłem go udowodnić. Wychwyciłem to przy rysowaniu wykresów funkcji wielomianowej. Może jest ktoś kto potrafi napisać dowód tego twierdzenia. Jednakże stawiam że jest on bardzo długi, zapewne na kilka stron A4. Pozdrawiam

ICSP: Myślę że aby to udowodnić trzeba wejść w zespolone.

iga: Dziękuję bardzo. To chociaż się nie dziwię, że o tym nie słyszałam. Jeszcze raz dzięki wielkie. Pozdrawiam.

ICSP: Trivial jestes

Trivial: Poniekąd.

ICSP: Jak widać masz zadanko

Trivial: Dowód A: Weźmy dowolny wielomian formy W(x) = ⁿ∑_i=0 a_ixⁱ. Zauważmy, że gdy n jest nieparzyste to zachodzą własności: lim_x→−∞ W(x) = −∞ oraz lim_x→+∞ W(x) = +∞ (dla a_n > 0) lim_x→−∞ W(x) = +∞ oraz lim_x→+∞ W(x) = −∞ (dla a_n < 0) Wynika z tego, że wykres wielomianu W(x) przecina oś Ox choć raz, co implikuje bezpośrednio istnienie przynajmniej jednego pierwiastka rzeczywistego wielomianu W(x).

ICSP: aha.

Trivial: A jeśli chodzi o to twierdzenie to: Weźmy np. wielomian (x−1)(x−3)². Ile ma pierwiastków rzeczywistych (jest 3. stopnia). To twierdzenie zadziała tylko wtedy, gdy liczysz pierwiastki krotne jako oddzielne.

Trivial: Dowód Twojego twierdzenia: Dowolny wielomian można zapisać jako iloczyn pewnej liczby rzeczywistej α, pewnej liczby dwumianów (x−x_i), gdzie x_i to pierwiastki rzeczywiste, oraz pewnej liczby trójmianów nierozkładalnych (x² + a_jx + b_j). Wielomian nieparzystego stopnia można zapisać jako iloczyn jednego dwumianu i pewnej ilości trójmianów. Niektóre z nich dadzą się rozłożyć, inne nie. Te które się rozłożą dadzą dwa pierwiastki rzeczywiste. Czyli liczba pierwiastków rzeczywistych jest formy 2k+1 (uwzględniając krotność).

Wezyr: No dobrze, ale i tak z tego nie wynika punkt B, że wielomian ma co najwyżej 1 pierwiastek rzeczywisty

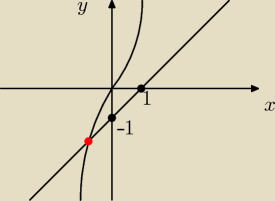
Trivial: Tak. Z tego twierdzenia nie wynika wcale B. Najłatwiej B udowodnić metodą graficzną (czyli przy okazji A). x²⁰¹¹ = x−1. Jedno miejsce przecięcia wskazuje na jeden pierwiastek rzeczywisty. C: można łatwo pokazać z twierdzenia o wymiernych pierwiastkach wielomianu, że jedynymi kandydatami na wymierne pierwiastki są x=±1, ale oba nie spełniają tego równania. D pokazał ICSP.

ICSP: a ja głupi przeczytałem A i B tak samo

Trivial:

teofrast: twierdzenie Kartezjusza pozwala oszacować liczbę pierwiastków dodatnich W(x): jest ich dokładnie 2 lub 0.; liczba pierwiastków ujemnych wynosi zaś z tego samego twierdzenia : dokładnie 1 (widać to na wykresie...) Teraz wystarczy « tylko » udowodnić na drodze analitycznej, że W(x) nie ma zer dodatnich.

Vax: To, że nie może mieć zer dodatnich można łatwo udowodnić rozpatrując 2 przypadki: 1*) x ∊ (0 ; 1> jednak wtedy: { x²⁰¹¹ > 0 { −x+1 ≥ 0 Czyli x²⁰¹¹ − x + 1 > 0 2*) x ∊ (1 ; +∞) jednak wtedy: x²⁰¹¹ − x > 0 więc tym bardziej x²⁰¹¹ − x + 1 > 0 Pozdrawiam.

ICSP: zer dodatnich

Vax: Inaczej dodatnich miejsc zerowych.

teofrast: Ubiegłes mnie Vax... bo zostałem wezwany na zupę... ale ja chciałem zrobić nieco inaczej: W(0) = 1, W(+∞) = +∞, podejrzewamy,że W(x) nie zmienia znaku na (0, +∞). W'(x) = (x−1)Q(x) gdzie Q(x) jest nierozkładalny w R. ⇒ W jest malejący dla x<1 i rosnący dla x>1⇒dla x= 1 jest jedune minimum i jest to jedyny punkt ekstremalny. W(1) = 1 zatem najmniesza warościa na (0, +∞) jest 1 (osiagana zarówno dla x=1 jak i x=0), przeto W(x)>0 dla x∊(0+∞), cnd. Pozdrawiam, <t>

Vax: Teofrast, wydaje mi się, że Twoje rozumowanie jest błędne.. po pierwsze 1 nie jest miejscem zerowym W'(x), więc nie możemy napisać W'(x) = (x−1)Q(x), po 2 stwierdzenie, że minimalna wartość W(x) dla x ∊ (0 ; +∞) to 1 jest błędne, wystarczy wziąć dowolne x ∊ (0 ; 1), wtedy W(x) = x²⁰¹¹−x+1 < 1. Pozdrawiam.

teofrast: Oczywiscie, masz rację, szanowny i nieomylny Vaxie... Pospieszyłem sie...Wszystko przez to spóźnienie na obiad... Nieraz sie w matematyce tak zdarza, że się człowiek myli. Aby wyjśc z tego z twarzą postaram sie rozumowanie uratować. W'(x) = 2011x²⁰¹⁰ − 1 = 2011 ( x²⁰¹⁰ − ¹₂₀₁₁ ) = = 2011 [ x − ¹₂₀₁₁^{1₂₀₁₀}] Q(x). Ponieważ wykładnik 2010 jest parzysty, zatem wspólczynniki Q(x) są dodatnie i cały wielomian Q(x) przyjmuje wartości dodatnie dla x > 0. W'(x) = 0 dla x = x_o = ¹₂₀₁₁^{1₂₀₁₀}. Widzimy, że W' < 0 dla x < x_o i W' > 0 dla x > x_o . Zatem w x_o jest minimum. Bezpośrednim rachunkiem sprawdzamy, że W(x_o) = W ( ¹₂₀₁₁^{1₂₀₁₀}) > 0 . Zatem W( x ) > 0 dla x∊(0+∞), à propos obliczania ilości pierwiastków: na ubiegłorocznym egzaminie wstępnym do jednej z wyższych szkół inżynierskich we Francji pojawiło się takie oto zadanie: « Na dodze analitycznej ustalić liczbę pierwiastków równania x ln | x + 1 | − 1 = 0. » Pozdrawiam, <t>