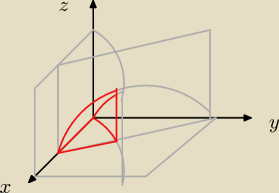
Obliczyć objętość bryły zawartej między powierzchniami: siwy: Obliczyć objętość bryły zawartej między powierzchniami: paraboloidą hiperboliczną z=xy, walcem parabolicznym y=√x, płaszczyznami x+y=2 y=0 z=0. Bardzo proszę o pomoc, to znaczy o wyjaśnienie w miare możliwości co i jak należy tu wykonać

Trivial: Trzeba narysować, zapisać całkę, dobrać granice i policzyć.

Trivial:

Trivial: z zmienia się od z=0 do z=xy, y zmienia się od y=0 do y=√x aż do pewnego x₀, który jest miejscem przecięcia powierzchni y=√x i x+y=2. Potem y zmienia się od y=0 do y=2−x. x zmienia się od x=0 do x=x₀, a potem od x=x₀ do x=2. Wyliczmy x₀. Spełnia on układ równań:

⎧	y=√x
⎩	x+y=2	, czyli

x + √x = 2 Niech t = √x, t≥0. t² + t − 2 = 0 Δ = 1+8 = 9, √Δ = 3.

	−1±3
t =		, ale t≥0, czyli ostatecznie:
	2

t = 1. √x=1 → x₀ = 1 Wyliczyliśmy x₀. Zapiszemy teraz całkę. Jeżeli naszą bryłę nazwać Ω, to jej objętość wynosi: 1 √x xy 2 2−x xy |Ω| = ∭dxdydz = ∫dx∫dy∫dz + ∫dx ∫dy ∫dz = ... Ω 0 0 0 1 0 0