Wyznacz punkt C
mitchell:
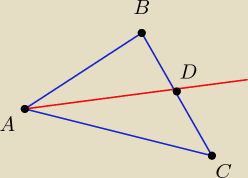
A (1,−4)
B (6,1)
D (4,5)
prosta AB x−y−5=0
prosta BC 2x+y−13=0
prosta AD jest dwusieczną kąta BAC 3x−y−7=0
Jak wyznaczyć punkt C?
Sławek:
Punkt C to punkt wspólny prostych AB i BC.
Należy rozwiązać układ równań liniowych:
Rozwiązujemy układ np. metodą podstawiania.
Odp. C(6,1)
Jack:
1) liczę tgα, gdzie α to kąt między prostymi AB i AD.
| | 1−3 | | 1 | |
tgα= |
| =− |
| <0 − odpada, ponieważ α<π/2.
|
| | 1+1*3 | | 2 | |
| | 3−1 | | 1 | |
tgα= |
| = |
| >0 więc ok.
|
| | 1+3*1 | | 2 | |
| | 1 | |
2) Stąd tg kąta między AD i AC równy również |
| . Niech prosta przechodząca przez A i C |
| | 2 | |
będzie opisana równaniem: y=a
1x+b
1
| 1 | | a1−3 | | 3−a1 | |
| =tgα= |
| ⇒ a1=−7 (przypadek gdy liczymy tgα= |
| prowadzi do |
| 2 | | 1+3a1 | | 1+3a1 | |
wcześniejszej prostej)
3) Zatem y=−7x+b
1. Mając punkt A(1,−4) liczymy, że b
1=3. Więc y=−7x+3.
4) Pozostaje policzyć przecięcie prostych:
y=−7x+3
y=−2x+13
−5x=10 ⇒ x=−2 i y=17. Więc C(−2,17)