PROblem
TOmek: ICSP , jak masz czas to wrzuć jakies zadanko

21 lip 14:01
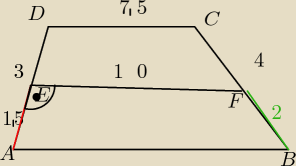
ICSP: Ramiona trapezu mają długości 3cm oraz 4cm, krótsza podstawa ma długość 7,5cm a długość odcinka
łączącego środki ramion jest równa 10cm. Oblicz długość dłuższej podstawy i pole tego trapezu.
21 lip 14:04
ICSP: [P{Trivial]] albo
Godzio dla was mam inne zadanko

Do policzenia w pamięci

21 lip 14:55
ICSP: Trivial*
21 lip 14:56
Trivial: Już się boję...
21 lip 14:56
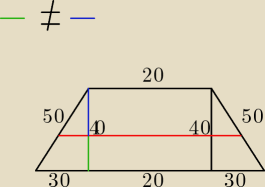
ICSP: Działkę budowlaną w kształcie trapezu o bokach 50m,20m,50m,80m podzielono na dwie części o
równej powierzchni płotem równoległym do podstaw trapezu. Jaka jest długość płotu
rozdzielającego obie działki?
21 lip 14:57
Trivial: 50 m? Nie pamiętam tego wzoru dobrze, ale chyba 50 m.

21 lip 15:01
Trivial: nie 50m. Źle to przeczytałem.
21 lip 15:02
ICSP: Widać że jesteś matematykiem

Problemy z czytaniem...
21 lip 15:05
Patryk: 80+20 :2 ?
21 lip 15:07
ICSP: Nie

21 lip 15:10
Godzio: 10√34 ?
21 lip 15:18
ICSP: Brawo
Godziu
W pamięci?
21 lip 15:19
Tes:
hm..
21 lip 15:21
Godzio:
Prawie że

jakoś odruchowo dodałem 400 + 6400 i podzieliłem na dwa na kalkulatorze,
spierwiastkowałem w pamięci

21 lip 15:22
ICSP: banalne zadanko

Oczywiście o najszybszym sposobie rozwiązanie nie wspomną w liceum bo po co?
21 lip 15:26
Godzio:
To ja w takim razie mogę dać zadanko TOmkowi analogiczne do tego co dał nam ICSP:
Jaką długość ma odcinek, w trapezie o podstawach a i b, dzielący go na dwa trapezy o równych
polach, a do tego równoległy do podstaw
21 lip 15:26
Godzio:
No właśnie

Jedynie co w szkole poznałem to odcinek łączący środki ramion ...
21 lip 15:27
Trivial:
Już widzę wszystkich ludzi budujących domy na działkach w kształcie trapezów o równych polach i
podzielonych na dwie części o płocie długości x.

21 lip 15:29
ICSP: a najlepsze jest to że znam ten wzór ale nie potrafię go wyprowadzić

. Tzn. bez tego wzoru nie
rozwiązałbym zadania

21 lip 15:30
Trivial:
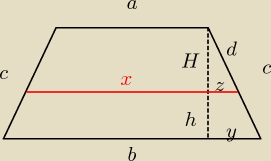
(a+x)H = (b+x)h
Teraz rozwiązać i masz wzór.

21 lip 15:36
ICSP: Mam jeszcze jedno zadanko. Według mnie bardzo interesujące

21 lip 15:42
ICSP: ale ono zostanie dla Tomka

21 lip 15:42
Godzio: 
21 lip 15:43
ICSP: No dobrze. Podam treść. Tylko jest to zadanie z pierwszej klasy liceum. Nie było jeszcze
trygonometrii więc nie wolno używać wzór redukcyjnych itd.
Trapez ABCD ma wysokość równą 10, a bok AB jest dłuższą podstawą. Oblicz pole trapezu jeśli:
∡DAB = 30o
∡ABC = 75o
∡ACB = 90o
21 lip 15:46
TOmek:
Ramiona trapezu mają długości 3cm oraz 4cm, krótsza podstawa ma długość 7,5cm a długość odcinka
łączącego środki ramion jest równa 10cm. Oblicz długość dłuższej podstawy i pole tego trapezu.
−−−−−−−−−−−−−−−−−−−−−−−−−−−
mam pytanie czy kąty AEF i BFE = 90
0
21 lip 16:14
ICSP: nie. Tak by było w prostokącie lub kwadracie. Pamiętaj że jest wzór na długość odcinka
łączącego środki ramion.
21 lip 16:17
Godzio:
TOmek rada doświadczonego kolegi, przysiądź do teorii, bo tutaj widać znaczące braki
21 lip 16:20
21 lip 16:20
TOmek:
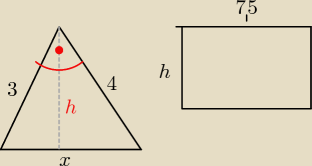
x=12,5−7,5=5
3,4,5 to pitagoras
3*4/2=6
5*h=3*4 porównanie pól
wiadomo

lece na trening
21 lip 16:41
TOmek: Godzio mam taką dużą bazę definicji i raz po raz sobie to wszystko odświeżam bo troche tego
jest

21 lip 16:41
ICSP: ten trójkąt i to z to co to jest

21 lip 16:42
TOmek:
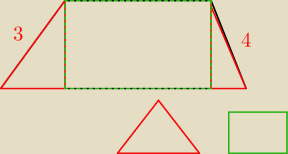
21 lip 19:14
ICSP: oo bardzo interesujące rozwiązanie

Nie wpadłbym na to. Oczywiście h dobrze wyliczone. Zostało
jeszcze pole i możesz brać się za drugie zadanko.
21 lip 19:20
TOmek: te "Trapez ABCD .. tak?
21 lip 19:33
ICSP: Taa

21 lip 19:34
TOmek: a mogę uzyć np: sin60 =

21 lip 19:49
TOmek: nie potrzebne jest mi to

21 lip 19:50
TOmek:
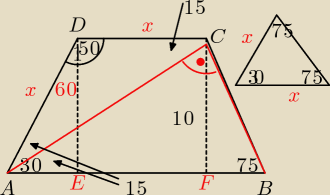
Trapez ABCD ma wysokość równą 10, a bok AB jest dłuższą podstawą. Oblicz pole trapezu jeśli:
∡DAB = 30
∡ABC = 75
∡ACB = 90
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
P=(AB+DC)*5
BAC=90−75=15
czyli AC jest dwusieczną.
* liczę odcinek ACD=180−(75+90)=15
* liczę ADC 180−30=150
−−−−−−−−−−−−−−
AC*CB=FC*AB /:FC
−−−−−−−−−−
rysuje trójkąt z "boków trapezu" i dowiadujemy się ,ze jest równoramienny i
AE+FB=AD
−−−−−−−−−−−
dowiadujemy się także ,ze trójkąt ADC jest równoramienny i
AD=DC
−−−−−−−−−−−−−
trójkąt AED to 30,60,90
więc AE=10
√2
AD=20
−−−−−−−−−−−−−−
biorąc pod uwagę wszystkie informacje obliczamy pole trapezu
P=(DC+AB)*5
DC=AD=20
odicnek AB składa sie z AB+FB(jest to równe 20) i odcinka +EF (który =20)
czyli AB=40
P=300
21 lip 19:54
ICSP: No nieźle. Muszę przyznać że nieźle

21 lip 19:59
Godzio:
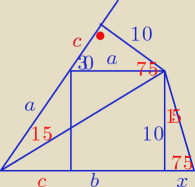
| x | | 10 | | 10 | |
| = |
| ⇒ x = |
| = 20 − 10√3 |
| 10 | | 20 + 10√3 | | 2 + √3 | |
b = a + c + x = 20 + 10
√3 + 20 − 10
√3 = 40
P = 300
Nie wiem czy krótsza metoda, ale w ten sposób można wykorzystać, że prosta AC jest dwusieczną
kąta DAB

21 lip 20:14
TOmek: Własnie przypominam sobie trygonometrie i mam jedno takie zadanko:
| | 1 | | 1 | |
Wykaż ,ze |
| + |
| < 4 |
| | log32 | | log52 | |
próbowałem to zrobić tak ,ale coś nie idzie dalej:
| 1 | | 1 | |
| + |
| < 4 / log32 |
| log32 | | log52 | |
| | log32 | |
1+ |
| =4*log32 /*log52 |
| | log52 | |
log
52+log
32 < 4*log
32*log
52
próbowałem tu w log
52 zmienić podstawę logarytmu ale nic nie pasuje..
Proszę o wskazówki.
21 lip 20:23
TOmek: przypominam sobie *logarytmy

21 lip 20:23
21 lip 20:26
TOmek:
log
23+log
25<4
log
2(3*5)<4
log
215 < 4
i co dalej?
I takie pytanko ten wzór zawsze 'działa'?
21 lip 20:29
Godzio:
A czemu ma nie działać ?
4 = log216
log215 < log216
15 < 16
21 lip 20:33
TOmek: dzieki, logarytmy nie mam za dobrze ogarnięte, a cos czuje ,ze bedą na maturze ,bo dawno nie
były
21 lip 20:37
Trivial:
Godzio, nie zawsze.

Zobacz co otrzymasz dla log
a1. Dla dowolnego a spełniającego założenia podstawy logarytmu.

21 lip 20:41
21 lip 20:44
TOmek: Sląsk Wrocław gra zaraz , zlituj sie

21 lip 20:46
Trivial: Bez przesady
ISCP, takie tanie sensacje to nie z nami.

21 lip 20:50
TOmek: zapodajcie jakieś zadanko

mile widziany wielomiany, planimertria, stereometria, ciągi

21 lip 21:23
Godzio:
@
Trivial
To taki oczywisty przypadek, którego nie trzeba tłumaczyć

21 lip 21:40
Godzio:
I zadanie z ciągów:
Suma n początkowych wyrazów ciągu arytmetycznego (an) wyraża się wzorem Sn = 2n2 + n dla n ≥
1. Oblicz sumę 50 początkowych wyrazów tego ciągu o numerach parzystych:
a2 + a4 + ... + a100
21 lip 21:48
TOmek: a
n=S
n−S
n−1
a
n=2n
2 + n−2(n−1)
2+n=2n
2+2n+2(n
2−2n+1)=2n
2+2n+2n
2−4n+2=4n
2−2n+2
a
n=4n
2−2n+2
tworzymy sobie nowy ciąg w którym
a
2 ciągu a
n = a
1 ciągu a
f
a
100 ciągu a
n = a
50 ciągu a
f
a
2=16−2=14
a
100=202
czyli w tym naszym nowym ciągu a
f
a
1=14
a
50=202
jaki masz wynik

?
21 lip 22:44
TOmek: jutro loookne czy dobrze, teraz ide kimać , Dobranoc!
21 lip 22:47
Pepsi2092: Mi wyszło 7650 ale nie wiem czy dobrze

21 lip 23:08
Pepsi2092: Aj dałem ciała już widzę i
TOmek też ma zły wynik

21 lip 23:11
ICSP: Tomku ciąg arytmetyczny jest funkcją liniową a nie kwadratową

S
n = 2n
2 + n
S
1 = 3
S
2 = 10 a
2 = 7
S
3 = 21 a
3 = 11
z tego mogę odczytać ze ten ciąg ma wzór ogólny : a
n = 4n − 1
teraz utworzymy ciąg b
n który będzie miał następujące własności:
b
1 = a
2
b
2 = a
4
b
50 = a
100
a
2 = 7 = b
1
a
100 = 399 = b
50
S
50 = (b
1 + b
50) * 25 = (7 + 399)*50 = 20300

21 lip 23:18
Pepsi2092: 10150

Ale wszystko dobrze liczyłeś, tylko ostatnia linijka mi się coś nie zgadza

21 lip 23:23
ICSP: Mój błąd. JUż łądnie skróciłem tylko nie wiem czemu napisałem 50:( Śpiący już chyba jewstem:(
21 lip 23:24
ICSP: poprawiam:
(7+399) * 25 = 10150
21 lip 23:25
Pepsi2092: Nie ma się co przejmować
ICSP przecież wszystko było elegancko zrobione

Ja teraz mam
zamiar ogarnąć na własną rękę całą trygonometrię, tzn chodzi mi o rozszerz w liceum, możesz mi
doradzić od czego mam zacząć?

21 lip 23:29
ICSP: Zacznij od definicji oraz zadań z podstawy. Zrób tak z 15. Później to samo tylko dla wszystkich
ćwiartek. Musisz mieć to dobrze opanowane gdyż bez tego nie ruszysz dalej. Później tożsamości(
te bardziej zaawansowane i wzory redukcyjne + funkcje trygonometryczne sumy i różnicy kątów)
Następnie uczysz się rysować i przekształcać wykresy. Przedostatnim korkiem są tożsamości i
kończysz równianami i nierównościami trygonometrycznymi.
21 lip 23:33
Pepsi2092: Oka, wielkie dzięki. Od sierpnia zaczynam i w razie jakiś problemów będę prosił o pomoc. A
teraz lece w kimono

Narciarz

21 lip 23:35
TOmek: no to ogolnie dobrze zrobiłem tylko na koncu literowka

22 lip 14:33
TOmek: ojej, pomylilem moj post z postem ICSP , pospiech, ;0
22 lip 14:35
TOmek: taki sam jak ICSP miałem pomysł tylko nie potrafie odejmować Sn od Sn−1
22 lip 14:38
Godzio:
Co do mojego zadania
TOmek mały błąd na początku,
S
n − S
n − 1 = 2n
2 + n − 2(n − 1)
2 −
(n − 1) 
22 lip 15:58
TOmek: na maturze bym 25 razy sprawdził czy nie ma błędu rachunkowego, najwazniejsze, ze był pomysl i
dobry

22 lip 19:27
ICSP: to możesz sobie zapamiętać. Po połączeniu kropek wykresu ciągu arytmetycznego powstanie funkcja
liniowa.
22 lip 19:35

 Do policzenia w pamięci
Do policzenia w pamięci

 Problemy z czytaniem...
Problemy z czytaniem...

 W pamięci?
W pamięci?
 hm..
hm..
 jakoś odruchowo dodałem 400 + 6400 i podzieliłem na dwa na kalkulatorze,
spierwiastkowałem w pamięci
jakoś odruchowo dodałem 400 + 6400 i podzieliłem na dwa na kalkulatorze,
spierwiastkowałem w pamięci 
 Oczywiście o najszybszym sposobie rozwiązanie nie wspomną w liceum bo po co?
Oczywiście o najszybszym sposobie rozwiązanie nie wspomną w liceum bo po co?
 Jedynie co w szkole poznałem to odcinek łączący środki ramion ...
Jedynie co w szkole poznałem to odcinek łączący środki ramion ...

 . Tzn. bez tego wzoru nie
rozwiązałbym zadania
. Tzn. bez tego wzoru nie
rozwiązałbym zadania





 Ramiona trapezu mają długości 3cm oraz 4cm, krótsza podstawa ma długość 7,5cm a długość odcinka
łączącego środki ramion jest równa 10cm. Oblicz długość dłuższej podstawy i pole tego trapezu.
−−−−−−−−−−−−−−−−−−−−−−−−−−−
mam pytanie czy kąty AEF i BFE = 900
Ramiona trapezu mają długości 3cm oraz 4cm, krótsza podstawa ma długość 7,5cm a długość odcinka
łączącego środki ramion jest równa 10cm. Oblicz długość dłuższej podstawy i pole tego trapezu.
−−−−−−−−−−−−−−−−−−−−−−−−−−−
mam pytanie czy kąty AEF i BFE = 900
 x=12,5−7,5=5
3,4,5 to pitagoras
3*4/2=6
5*h=3*4 porównanie pól
x=12,5−7,5=5
3,4,5 to pitagoras
3*4/2=6
5*h=3*4 porównanie pól
 lece na trening
lece na trening



 Nie wpadłbym na to. Oczywiście h dobrze wyliczone. Zostało
jeszcze pole i możesz brać się za drugie zadanko.
Nie wpadłbym na to. Oczywiście h dobrze wyliczone. Zostało
jeszcze pole i możesz brać się za drugie zadanko.



 Trapez ABCD ma wysokość równą 10, a bok AB jest dłuższą podstawą. Oblicz pole trapezu jeśli:
∡DAB = 30
∡ABC = 75
∡ACB = 90
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
P=(AB+DC)*5
BAC=90−75=15
czyli AC jest dwusieczną.
* liczę odcinek ACD=180−(75+90)=15
* liczę ADC 180−30=150
−−−−−−−−−−−−−−
AC*CB=FC*AB /:FC
Trapez ABCD ma wysokość równą 10, a bok AB jest dłuższą podstawą. Oblicz pole trapezu jeśli:
∡DAB = 30
∡ABC = 75
∡ACB = 90
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
P=(AB+DC)*5
BAC=90−75=15
czyli AC jest dwusieczną.
* liczę odcinek ACD=180−(75+90)=15
* liczę ADC 180−30=150
−−−−−−−−−−−−−−
AC*CB=FC*AB /:FC




 Zobacz co otrzymasz dla loga1. Dla dowolnego a spełniającego założenia podstawy logarytmu.
Zobacz co otrzymasz dla loga1. Dla dowolnego a spełniającego założenia podstawy logarytmu. 



 mile widziany wielomiany, planimertria, stereometria, ciągi
mile widziany wielomiany, planimertria, stereometria, ciągi 

 ?
?


 Sn = 2n2 + n
S1 = 3
S2 = 10 a2 = 7
S3 = 21 a3 = 11
z tego mogę odczytać ze ten ciąg ma wzór ogólny : an = 4n − 1
teraz utworzymy ciąg bn który będzie miał następujące własności:
b1 = a2
b2 = a4
b50 = a100
a2 = 7 = b1
a100 = 399 = b50
S50 = (b1 + b50) * 25 = (7 + 399)*50 = 20300
Sn = 2n2 + n
S1 = 3
S2 = 10 a2 = 7
S3 = 21 a3 = 11
z tego mogę odczytać ze ten ciąg ma wzór ogólny : an = 4n − 1
teraz utworzymy ciąg bn który będzie miał następujące własności:
b1 = a2
b2 = a4
b50 = a100
a2 = 7 = b1
a100 = 399 = b50
S50 = (b1 + b50) * 25 = (7 + 399)*50 = 20300
 Ale wszystko dobrze liczyłeś, tylko ostatnia linijka mi się coś nie zgadza
Ale wszystko dobrze liczyłeś, tylko ostatnia linijka mi się coś nie zgadza
 Ja teraz mam
zamiar ogarnąć na własną rękę całą trygonometrię, tzn chodzi mi o rozszerz w liceum, możesz mi
doradzić od czego mam zacząć?
Ja teraz mam
zamiar ogarnąć na własną rękę całą trygonometrię, tzn chodzi mi o rozszerz w liceum, możesz mi
doradzić od czego mam zacząć?
 Narciarz
Narciarz


