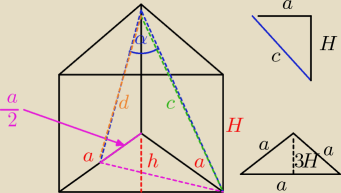
PROblem TOmek: W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej jest równe sumie pól obu podstaw. Oblicz kosinus kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej. −−−−−−−−−−−−−−−−−−−−−−−−−−−−

	a*h
3*a*H=		*2
	2

3aH=ah /a 3H=h c²=H²+a²

	a2
d2=		+H2
	4

w podstawie mamy trójkąt równoramienny, więc h=3H raczej tw. cos nie da mi wyniku, także czekam na jakieś wskazówki.

	a2		a2
3H2=H2+a2+		+H2−2*√H2+a2*√		+H2*cosα
	4		4

najlepiej było by za pomocą "H" określić "a".. Lecz nie wiem jak

ICSP: w podstawie jest trójkąt równoboczny.

ICSP: masz odpowiedzi?

	2√13
cosα =		?
	13

TOmek: dobrze, tylko jak Ci to wyszło?

ICSP: a to akurat nie trudne.

a2√3		√3
	= 3aH ⇔ H =		a
2		6

Teraz twoim zadaniem jest wyliczenie d ,c oraz h d i c wyliczysz z twierdzenia Pitagorasa.

	√39
c=		a
	6

	√3
d =		a
	3

h jest wzorem na wysokość trójkąta równobocznego. Później stosujesz twierdzenie cosinusów. Wyniki do odpowiednich odcinków już masz tak więc będziesz wiedział gdzie ewentualnie bład popełniłeś. Ja będę za jakieś 30min.

TOmek: wystarczyła Twoja pierwsza linijka i juz wiem , co dalej.

ICSP: "a to akurat nie trudne" − to wystarczyło?

TOmek: wiesz o co Chodzi

TOmek: "najlepiej było by za pomocą "H" określić "a".. Lecz nie wiem jak "

Hania: A wystarczyło policzyć cosinus ze stosunku d przez c. Przecież trójkąt o bokach c, d ,h jest prostokątny . Nie trzeba liczyć h. Troszkę szybciej.