 Tomku
Tomku Gdzie jesteś
Gdzie jesteś W sześcianie, którego krawędź ma długość 1, połączono wszystkie wierzchołki dolnej podstawy z
jednym z wierzchołków górnej podstawy i w ten sposób otrzymano ostrosłup. Oblicz miarę kąta
zawartego między tymi ścianami bocznymi ostrosłupa które nie są prostopadłe do podstawy
W sześcianie, którego krawędź ma długość 1, połączono wszystkie wierzchołki dolnej podstawy z
jednym z wierzchołków górnej podstawy i w ten sposób otrzymano ostrosłup. Oblicz miarę kąta
zawartego między tymi ścianami bocznymi ostrosłupa które nie są prostopadłe do podstawy
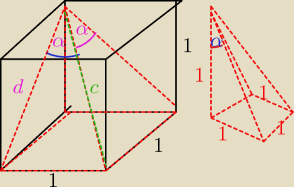 d2=2
d=√2
przekątna szescianu to a√3 = √3=c
z tw. cos
1=(√2)2+(√3)2−2*√3*√2*cosα
1=2+3−2√6*cosα
d2=2
d=√2
przekątna szescianu to a√3 = √3=c
z tw. cos
1=(√2)2+(√3)2−2*√3*√2*cosα
1=2+3−2√6*cosα
| −4 | |
=cosα | |
| −2√6 |
| 4*√6 | √6 | |||
cosα= | = | |||
| 12 | 3 |
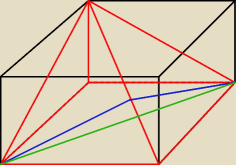 Mam nadzieję że ten rysunek ci pomoże. W tym zadaniu chodzi o kąt dwuścienny. Najpierw musisz
wymyśleć jak obliczyć długość odcinka niebieskiego. Tylko to jest w tym zadaniu problemem.
Mam nadzieję że ten rysunek ci pomoże. W tym zadaniu chodzi o kąt dwuścienny. Najpierw musisz
wymyśleć jak obliczyć długość odcinka niebieskiego. Tylko to jest w tym zadaniu problemem.
 Widok z lotu ptaka. Jak myślisz, który kąt został do wyboru?
Widok z lotu ptaka. Jak myślisz, który kąt został do wyboru? 
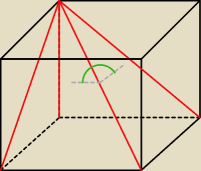 Kąt jest w środku ostrosłupa.
Kąt jest w środku ostrosłupa.

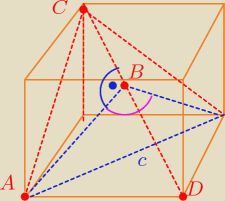 c=√2
jeśli prosta AB przecina CD pod kątem 900 to musi ona dzielić odcinek CD na 2 równe częsci
więc CB=BD
u tu na razie zakoncze bo nie wiem czy dobrze rozumuje
c=√2
jeśli prosta AB przecina CD pod kątem 900 to musi ona dzielić odcinek CD na 2 równe częsci
więc CB=BD
u tu na razie zakoncze bo nie wiem czy dobrze rozumuje

| √3 | |
=AB | |
| 2 |
| √3 | ||
|AB| ≠ | ||
| 2 |
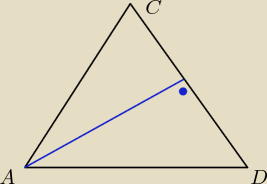 jesteś wstanie wypisać długości odcinków |AD| |AC| |CD|?
Dane z twojego rysunku.
jesteś wstanie wypisać długości odcinków |AD| |AC| |CD|?
Dane z twojego rysunku.
| niebieski | ||
sinADC = | ||
| AD |
| 1 | ||
cosADC= | ||
| √3 |
| √2 | ||
sinADC= | ||
| √3 |



| √6 | ||
niebieski = | . Teraz zostało jeszcze obliczyć ka z twierdzenia cosinusów. | |
| 3 |
| AB*CD | AC*AB | ||
= | /*2 | ||
| 2 | 2 |
| √2 | √6 | |||
AB= | = | |||
| √3 | 3 |


| √6 | √6 | √6 | √6 | |||||
2=( | )2+( | )2−2* | * | *cosα | ||||
| 3 | 3 | 3 | 3 |
| 6 | 6 | 12 | ||||
2= | + | − | *cosα | |||
| 9 | 9 | 9 |
| 12 | 12 | |||
2= | − | *cosα / | ||
| 9 | 9 |
| ||||||||||
=cos | ||||||||||
|
| 1 | ||
cos=− | ||
| 2 |
| 1 | ||
cosα = − | (cosinus ujemny − ćwiartka II) | |
| 2 |