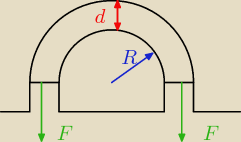
... Trivial: Witam. Mam problem z pewnym zadaniem z fizyki. Mianowicie: Zadanie. Chcemy zaprojektować budynek na powierzchni Księżyca taki, żeby utrzymywało się w nim ciśnienie P = 0.5 atm. Dach jest powierzchnią cylindryczną o promieniu R = 2 m. Jaka musi być siła F na metr długości, żeby dach się utrzymał? Jeśli ściana i dach są z materiału o wytrzymałości S = 2*10⁹ N/m², to jaka musi być minimalna dopuszczalna grubość d? (Wytrzymałość jest to maksymalna siła na jednostkę powierzchni, którą można przyłożyć do pręta z danego materiału bez trwałej deformacji ani rozerwania). W odpowiedziach podali tylko, że d = 5*10⁻⁵ m.

ziomek: spróbuj zarejestrować się na fizyczny.net tam na bank jakiś człowiek przeglądający forum udzieli Ci wskazówek jak to zrobić Mała szansa na to że tutaj ktoś rozkmini twoje zadanie a na tamtejszym forum takie zadanka to standard i nikt nie powinien mieć problemów z tym.Ale nie proś o to żeby ktoś za Ciebie rozwiązał bo za to są bany. Proś o wskazówki jak to zrobić

Trivial: Za dużo wysiłku trzeba włożyć, żeby się zarejestrować. Będę czekał aż wpadnie tutaj jakiś fizyk.

ziomek: Poczekaj wieczorem wrzucę ze swojego konta to zadanie. Zobaczymy co powiedzą fizycy.

Trivial: Czy fizycy przemówili?

ziomek: poczekaj chwile jakieś 20 min temu zadanie wrzuciłem.

Trivial: To już jutro. Albo dziś, zależy jak patrzeć.

Jakub: Tak się zastanawiam nad tym zadaniem i mam dwa pytania. To jest zadanie ze zbioru dla licealistów czy studentów? Ten rysunek jest dołączony do treści, czy to jest już twoja interpretacja zadania?

ziomek: Fizycy powiedzieli że silę z definicji ciśnienia trzeba policzyć a "resztę" masz w treści... lipa... czekamy aż ktoś bardziej skory do pomocy odpowie :S No i co z rysunkiem ? Jakub zwrócił słusznie uwagę.

Trivial: To książka Jay'a Oreara dla studentów. Rysunek był dołączony. To czego nie umiem zrobić dotyczy tego jak policzyć d, siła z definicji rzeczywiście.

ziomek: "Trzeba wyliczyć siłę działającą na dach, ale to proste http://fizyczny.net/cgi-bin/mimetex.cgi?\varphi%20=%20Pl%20=%20P\cdot%20\pi%20R Używam φ żeby zaznaczyć, że jest to siła na jednostkę długości. Jak teraz wyliczyć d? http://fizyczny.net/cgi-bin/mimetex.cgi?S%20=%20\frac%20{\varphi}{l%27} No i dalej nie wiem. " tutaj jeden tak odpowiedział.

Trivial: Za wiele to nie rozjaśniło.

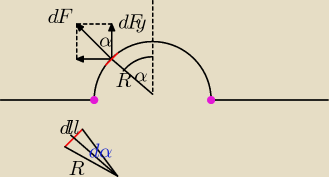
Jakub: Pytałem się, ponieważ to zadanie trzeba liczyć za pomocą całek, a w pierwszym momencie myślałem, że to zadanie dla liceum i się zdziwiłem. Oznaczę długość dachu jako "h". Wybrałem tę literę, ponieważ gdyby ten cylindryczny dach ustawić pionowo, to byłaby to wysokość cylindra (walca). Cały dach dzielę wzdłuż na nieskończenie wiele małych prostokątów o długości h i szerokości dl. Na rysunku zaznaczyłem jeden z nich kolorem czerwonym. Działa na niego siła pochodząca od ciśnienia powietrza, którą oznaczyłem jako dF. Na twoim rysunku zaznaczone zielono F to siła pochodząca od materiału, broniącego się przed rozerwaniem, tuż przy podłożu. Cały dach jest wypychany do góry przez powietrzne i najbardziej obciążona część to ta przy podłożu. Na moim rysunku zaznaczyłem ją za pomocą fioletowych kropek. Ten obszar musi wytrzymać całą siłę wypychającą dach do góry. Ta siła jest sumą wszystkich sił dF_y pochodzących od wszystkich prostokątów na jakie podzieliłem cylinder F = ∫dF_y = ∫dF*cosα = (*)

	F		dF
korzystam ze wzoru na ciśnienie p=		i mam p =
	s		ds

ds to pole tego wąskiego prostokąta (czerwonego), czyli ds = h*dl (*) = ∫p*ds*cosα = ∫p*h*dl*cosα = ph∫dl*cosα = (**) Na moim rysunku masz powiększony trójkąt. W rzeczywistości jest dużo węższy, ponieważ cylinder dzielimy na nieskończenie wiele bardzo wąskich prostokątów. Z tego trójkąta możemy ułożyć równanie

12dl
	= sin12dα
R

dla bardzo małych kątów, a takim jest dα, można napisać przybliżenie sindα ≈ dα

12dl
	= 12dα
R

dl = Rdα ^π₂ ^π₂ (**) = ph∫dl*cosα = ph∫cosαRdα = phR∫cosαdα = phR[sinα] = phR[sin^π₂ − sin0] = phR 0 0 Liczę całkę oznaczoną, gdzie granicę całkowania zaczynają się od α=0 (dF pionowo w górę) i kończą α=^π₂ (dF poziomo w lewo). Zauważ, że liczę tylko lewą połowę cylindra. Robię tak dlatego, że siła działająca na cały dach rozkłada się na dwie części przy podstawie dachu (fioletowe kropki). Mogę więc założyć, że lewa część odpowiada sile działającej na lewą połowę dachu. Siła z jaką jest "rozrywana" lewa podstawa dachu jest więc równa F = phR. Ta podstawa (fioletowa kropka) to wąski (o grubości d) pas metalu. Jego przekrój to prostokąt o długości h i grubości d. To on jest właśnie rozrywany przez ciśnienie działające na cały dach. Oczywiście w innych miejscach też działają siły, ale przy podstawie ta siła jest największa. Ze wzoru na wytrzymałość (wytrzymałość oznaczyłem jako W, a S to pole)

	F
W =		S−pole tego przekroju przy podstawie
	S

	F
W =
	d*h

	phR
W=
	d*h

	pR
W =
	d

	pR
d =
	W

Jak podstawisz p = 0,5atm = 0,5 * 101325Pa, R = 2m, W = 2*10⁹N/m² to wyjdzie w przybliżeniu odpowiedź z podręcznika. Typowe zadanie na rachunek całkowy z fizyki. Dawno już tego nie robiłem, więc mam nadzieję, że się nie pomyliłem PS Na rysunku przy czerwonym odcinku powinno być dl, a nie dll.

Trivial: Dziękuję bardzo. W tym podręczniku przyjmują, że 1 atm = 10⁵ Pa. Próbowałem całkować, ale uwzględniałem też F_x i to chyba nie była dobra droga.

Trivial: Spróbowałem zrobić sam od nowa i mi wyszło bez problemu. Teraz już będę wiedział, że mam brać tylko siłę F_y.