Zadanie dla Tomka na dziś.
ICSP: Wiem że nie lubisz trygonometrii tak więc troszkę ciebie podszkolimy

Oblicz sinx oraz cosx wiedzać że:
| | π | |
a) cos2x = 0,6 i x ∊ (0; |
| ) |
| | 2 | |
| | x | | 5 | | π | |
b) sin |
| = |
| i x ∊ ( |
| ; π) |
| | 2 | | 13 | | 2 | |
17 lip 20:29
TOmek: a) cos2x=cos
2x−sin
2x
cos
2x−sin
2x=0,6
cos
2x−(1−cos
2x)=0,6
cos
2x−1+cos
2x=0,6
2cos
2x=0,6+1
17 lip 21:40
TOmek: b) nie wiem jak to rozpocząc?
hmm?
sin2x=2sin*cos /4


17 lip 21:44
ICSP: Widać że tomek nie umie usunąć niewymierności z mianownika

17 lip 21:44
ICSP: Spróbuj narysować trójkąt równoramienny i jego wysokość. Zauważ na jakie kąty podzieli ona kąt
przy wierzchołku.
17 lip 21:44
17 lip 21:45
Trivial:
ISCP, nie zawsze trzeba usuwać, bo i po co.

17 lip 21:45
17 lip 21:47
Trivial:
Tomek, zauważ co mówi wzór: cos2α = cos
2α − sin
2α.

Teraz zapisz go trochę inaczej i już
masz obliczone.

17 lip 21:47
TOmek: a czy ten mój powyższy zapis
sin2x=2sin*cos /4
jest prawidłowy?
17 lip 21:52
TOmek:
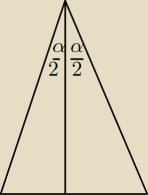
17 lip 21:55
ICSP: | | α | |
no i masz już kąt |
| . Teraz tylko wyznaczyć kąt α |
| | 2 | |
17 lip 21:56
TOmek: | | 10 | |
sin2=− |
| sin ∊(90,180) jest dodatni |
| | 13 | |
| | √10 | |
sin= |
| i usuwamy... |
| | √13 | |
dobrze idę?
17 lip 22:02
Godzio:
| | x | |
Musisz poprawić zapis koniecznie  Nie sin, nie cos, tylko sinx i cosx albo sin |
| , |
| | 2 | |
| | x | |
cos |
| , nie wiadomo o co Ci chodzi. Po za tym, nie sin ∊ (90,180) tylko x ∊ (90,180) |
| | 2 | |
Zapis jest równie ważny co rozwiązanie.
| | x | | sinxcosx | |
sin |
| = |
|  −− To wg Ciebie prawda ? |
| | 2 | | 2 | |
17 lip 22:11
Godzio:
| | 10 | |
I jeszcze jedno, doszedłeś do sprzeczności: sin2x = − |
| więc coś jest nie tak a czy |
| | 13 | |
sinx jest dodatni czy ujemny to nic tu nie zmienia
17 lip 22:12
TOmek: własnie sie pytałem czy to prawda i nie dostałem odpowiedzi. Teraz juz wiem ,ze nie ; 0..
17 lip 22:15
TOmek: | | x | |
to jak wziąc sie za to sin |
|  ? |
| | 2 | |
17 lip 22:15
Godzio:
Jeśli nie jesteś pewien to podstaw sobie 2−3 dowolne wartości x i sprawdź
Dla x = 60
o
| 1 | | √3 | |
| = |
| −− sprzeczność  |
| 2 | | 8 | |
17 lip 22:16
Godzio:
| | x | |
Szukasz sinx, masz dane sin |
| , znasz taki wzór: sin2x = sinxcosx, wykorzystaj go, tyle że |
| | 2 | |
17 lip 22:17
Godzio: sin2x = 2sinxcosx oczywiście
17 lip 22:17
TOmek: ok, będę pamiętał, fala krytyki ze strony Godzia

to znak ,ze musze lepiej ogarnąc
trygonometrie

nadal nie wiem co z tym trójątem równoramiennym ?
17 lip 22:18
Godzio:
Ja też nie wiem

Ale wiesz jak obliczyć ten sinx i cosx ?
17 lip 22:20
TOmek: tak myśle jak wykorzystać ostatni post Godzia
sin2x=2sin*cos
| | 2x | | x | | x | |
sin |
| =2sin |
| *cos |
| ale kombinuje, czuje ,ze to herezja  |
| | 2 | | 2 | | 2 | |
17 lip 22:21
TOmek: nie wiem jak zrobić to b)... nie mam pojecia..
17 lip 22:22
Trivial: Tomek, skorzystaj z mojej podpowiedzi.

17 lip 22:22
Godzio:
| | 2x | |
No i git !  sin |
| = sinx −− taki zapis lepszy |
| | 2 | |
| | x | | x | |
Mając sin |
| wyznaczysz cos |
| ? |
| | 2 | | 2 | |
17 lip 22:22
TOmek: Trivial, wybacz, ale nie potrafie : 0, sporobuje teraz iść drogą Godzia i idę spąc bo jutro na
5 do pracy...
17 lip 22:25
Godzio:
Hah

ja na 6

17 lip 22:26
Trivial:
A jak ci powiem, że
cos2α = 1−2sin
2α?

a teraz...
17 lip 22:26
Trivial: A ja jutro śpię do 10!
17 lip 22:26
Godzio:
Umiesz dobić człowieka

17 lip 22:28
TOmek: nie wiem czy tak można
| | x | | x | | 25 | |
sin( |
| )2cos( |
| )2= |
| |
| | 2 | | 2 | | 132 | |
| | x | | x | | 25 | |
sin( |
| )2(1−sin2 |
| )= |
| |
| | 2 | | 2 | | 132 | |
dobrze ide?
17 lip 22:30
Godzio:
Może lepiej się wyśpij i jutro spróbuj

17 lip 22:30
TOmek: dobry pomysł , Dobranoc, szykujcie sie na jutrrzejsze trygonometryczne herezje


17 lip 22:31
Trivial: 
17 lip 22:32
Trivial:
Moim sposobem:
cos2α = 1 − 2sin
2α
czyli
teraz to już proste.

17 lip 22:33
TOmek:
sin2x=2sin*cos
| | 2x | | x | | x | | x | | x | |
sin |
| =2sin |
| *cos |
| ⇒ sinx=2sin |
| *cos |
| ⇒ |
| | 2 | | 2 | | 2 | | 2 | | 2 | |
| | x | | x | | x | |
sinx=2sin |
| *cos |
| / 2cos |
| |
| | 2 | | 2 | | 2 | |
| | x | |
cos |
| liczę z wskazówki Trivial'a |
| | 2 | |
cos2x=1−2sin
2x z tego mamy
| | 2x | | x | | x | | x | |
cos |
| =1−2sin2 |
| ⇒ cosx=1−2sin2 |
| ⇒ no i jak z tego obliczyc cos |
| |
| | 2 | | 2 | | 2 | | 2 | |
18 lip 21:30
TOmek: hmm

18 lip 21:32
TOmek: zamotałem sie ...
18 lip 21:38
Trivial:
Masz dane:
| | x | | 25 | | 119 | |
cosx = 1 − 2sin2 |
| = 1 − 2* |
| = |
| . |
| | 2 | | 169 | | 169 | |
sinx można teraz z np. z jedynki trygonometrycznej.
18 lip 21:48
bart: ale go meczycie

18 lip 21:53
Trivial:
Nauczanie przez zadręczanie.

18 lip 21:56
TOmek: mądre

Jak macie jeszcze jakies zadanka z trygonometrii to chętnie sprobuje, tylko jutro bo
ide spac,
18 lip 21:59
bart: | | 1 | |
Uzasadnij ze sin10ocos20ocos40o= |
| |
| | 8 | |
18 lip 22:06
Vax: bart o ile dobrze pamiętam to zadanie już niedawno było

18 lip 22:14
ICSP: bart nie wiem ile razy już to zadanko robiłem...
18 lip 22:24
ICSP: to może ja dam zadanie z którym zapewne nikt sobie nie poradzi

Rozwiąż układ równań
6 różnymi metodami:
5x + 7y = 21
3x + 4y = 11
18 lip 22:50
Trivial:
1. Metoda zgadywania.
x=−7, y=8.
2. Metoda intensywnego wpatrywania się.
(ta metoda nie daje rozwiązań)
3. Metoda 'na chama'.
| | 21−7y | |
5x + 7y = 21 → x = |
| |
| | 5 | |
63 − 21y + 20y = 55
−y = −8
y = 8.
4. Metoda kombinowana.
5x + 7y = 21
3x + 4y = 11
2x + 3y = 10
x + y = 1
y = 8
x = −7
5. Metoda rosyjskiego uczonego Wyznacznikowa.
| | | |
detA = det | = 20 − 21 = −1. |
| | |
| | | |
detAx = det | = 84 − 77 = 7 |
| | |
| | | |
detAy = det | = 55 − 63 = −8 |
| | |
x = −7
y = 8.
6. Metoda trywialna.
Rozwiązanie tego układu jest trywialne − wynikiem jest x=−7, y=8.
7. Metoda dookoła świata
Niech x = rcosθ i niech y = rsinθ, wtedy:
5rcosθ + 7rsinθ = 21
| | sinθ | |
5rcosθ + 7r |
| cosθ = 21 |
| | cosθ | |
(1) rcosθ(5 + 7tgθ) = 21
3rcosθ + 4rsinθ = 11
(2) rcosθ(3 + 4tgθ) = 11
Dzielimy (1) przez (2):
55 + 77tgθ = 63 + 84tgθ
7tgθ = −8
| | rsinθ | | y | |
Ale tgθ = |
| , czyli tgθ = |
| ! Podstawiamy: |
| | rcosθ | | x | |
7y = −8x.
Podstawiamy to do równania 5x + 7y = 21 i mamy:
5x − 8x = 21
−3x = 21
x = −7.
czyli y = 8.
Metod jest wiele...
19 lip 00:35
 Oblicz sinx oraz cosx wiedzać że:
Oblicz sinx oraz cosx wiedzać że:







 Teraz zapisz go trochę inaczej i już
masz obliczone.
Teraz zapisz go trochę inaczej i już
masz obliczone. 

 Nie sin, nie cos, tylko sinx i cosx albo sin
Nie sin, nie cos, tylko sinx i cosx albo sin −− To wg Ciebie prawda ?
−− To wg Ciebie prawda ?  ?
?

 to znak ,ze musze lepiej ogarnąc
trygonometrie
to znak ,ze musze lepiej ogarnąc
trygonometrie  nadal nie wiem co z tym trójątem równoramiennym ?
nadal nie wiem co z tym trójątem równoramiennym ?
 Ale wiesz jak obliczyć ten sinx i cosx ?
Ale wiesz jak obliczyć ten sinx i cosx ?


 sin
sin ja na 6
ja na 6 
 a teraz...
a teraz...










 Jak macie jeszcze jakies zadanka z trygonometrii to chętnie sprobuje, tylko jutro bo
ide spac,
Jak macie jeszcze jakies zadanka z trygonometrii to chętnie sprobuje, tylko jutro bo
ide spac,


 Rozwiąż układ równań 6 różnymi metodami:
5x + 7y = 21
3x + 4y = 11
Rozwiąż układ równań 6 różnymi metodami:
5x + 7y = 21
3x + 4y = 11