zadanko TOmek: ICSP , zadanko please

Trivial: Hej tomek, zobacz na temat, który ma 61 odpowiedzi. Tam znajdziesz zadanie.

TOmek: bez przesady, to hardcore

Trivial: Promień podstawy stożka jest dwa razy dłuższy od promienia kuli wpisanej w ten stożek. Oblicz cosinus kąta rozwarcia stożka. Nie jest takie trudne.

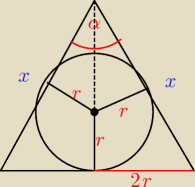
TOmek: 2r−promień stożka układ równań 4r²=x²+x²−2x*2r*cosα

	x2sinα
2r=
	2x+2r

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	x2sinα
2r=		/*2x+2r⇒
	2x+2r

2r(2x+2r)=x²sinα ⇒ 4r²+4xr=x²sinα⇒ 4r²=x²sinα−4xr 4r²=x²+x−2*2r*cosα x²sinα−4xr=x²+x²−2x*2r*cosα ⇒ x²sinα−4xr=2x²−2x*2r*cosα /:x xsinα−4r=2x²−2x*2r*cosα /2x²−2x*2r

	x*sinα−4r
cosα=
	2x−4xr

to zadanie przewyższa moje mozliwosci , jesli sam ICSP miał problem, wybaczcie, to hard

ICSP: dawaj Pomyśl a myślę że znajdziesz rozwiązanie. Jak nie uda ci się do 23:15 zrobię ci pomocniczy rysunek

TOmek: dzisiaj naprawdę nie dam rady, jestem zmęczony po całym tygodniu, myślałem ,ze dacie jakies łatwe zadanko na polepszenie humoru, a tu jak zwykle by mnie zdołowac

ICSP: już niedługo będziesz robił takie zadanka bez problemu

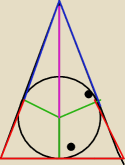
ICSP: opis: czerwony odcinek − 2R (w podstawie są dwa czerwone odcinki) niebieski odcinek − x zielony odcinek R różowy odcinek − y Oczywista oczywistość: x − 2y + 2R = 0 Podpowiedź: Zauważ że niektóre trójkąty są podobne. Z podobieństwa ułożysz drugie równaniu i pójdzie już z górki.

Trivial:

23
	?
25

ICSP:

Trivial: Mam błąd w jednym miejscu, zaraz poprawię.

Trivial:

16
	.
25

ICSP:

Trivial: Ahh... śpię...

7
	.
25

ICSP: Teraz czekamy aż jutro Tomek pokaże nam sposób rozwiązania

Trivial: Btw nie korzystałem z twojej metody. Wszystko wyszło algebraicznie, a nie z rysunku.

ICSP: już to widzę. Pewnie z kilka stron A4 Chociaż chętnie zobaczę tą twoją algebrę

Trivial: Pisać?

ICSP: Lecz to już jutro

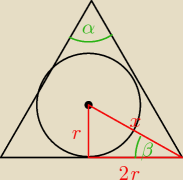
Trivial: Mam to rozwiązane na skrawku kartki, jutro zgubię. Piszę! Uwaga dla Tomka: NIE PATRZ W DÓŁ! cosα = ? 4β + α = 180^o

	α
β = 45o −		.
	4

4r² + r² = x² x = √5r

	r		r		1
sinβ =		=		=
	x		√5r		√5

	α		α		α
sinβ = sin(45o−		) = sin45ocos		− sin		cos45o =
	4		4		4

	1		α		α
=		(cos		− sin		)
	√2		4		4

	α		α		√2
cos		− sin		=		/2
	4		4		√5

	α		α		α		α		2
cos2		+ sin2		− 2cos		sin		=
	4		4		4		4		5

	α		2
1 − sin		=
	2		5

	α		3
sin		=		/2
	2		5

	α		9
sin2		=		.
	2		25

	α		α		α
cosα = cos2		− sin2		= 1 − 2sin2		.
	2		2		2

	2*9		18		7
cosα = 1 −		= 1 −		=		.
	25		25		25

Jack: od razu lepiej

ICSP: Skrawek papieru Żarty sobie ze mnie stroisz?

ICSP: Kto ma uprawnienia do edytowania tego forum?

Trivial: No mam mini rysunek i skrótowe przekształcenia. Zajęło pół kartki a5.

ICSP: ja nie lubię się tak w trygonometrii bawić. Do dzisiaj nie wiem jak rozwiązać jeden przykład który zrobiłem wzorem ponad licealnym:(

Trivial: Jest godzina 00:09. Dawaj ten przykład!

Trivial: Jak się zna wzory trygonometryczne, to łatwo wychodzi wszystko.

ICSP: sin4x = cos2x

Trivial: sin4x = cos2x 2sin2xcos2x = cos2x

	1
cos2x = 0 lub sin2x =
	2

...

ICSP: nieee. Udowodnij że sin4x = cos2x

ICSP: To nie może być takie proste

Trivial: Ale to nie prawda, przed chwilką pokazałem.

Trivial: nieprawda* ....

ICSP:

	1
ja dotarłem do momentu sin2x =		i tutaj się zaczęło Jutro napiszę moje obliczenia
	2

Trivial: ok.

ICSP: rozważmy równanie:

	1
sin2x =		.
	2

	1
2sinxcosx =
	2

	1
sinxcosx =
	4

	1
sin2xcosx =
	16

	1
sin2x(1−sin2x) −		= 0
	16

	1
−sin4x + sin2x −		= 0
	16

t = sin²x (t ∊ (0;1>

	1
−t2 + t −		= 0
	16

	3
Δ =
	4

	√3
√Δ =
	2

	√3   −1 +   2		√3   1 −   2
t1 =		=
	−2		2

t₂ = sprzeczne z założeniem

	√3   1 −   2		√3   1 −   2		√3   1 −   2
t1 =		⇔ sinx = √		v sinx = − √
	2		2		2

Tam są pierwiastki nie wiem czemu nie chcą wyjść.

	√3   1 −   2
sinx = √		⇔ x = 15o
	2

	√3   1 −   2
sinx = − √		⇔ x = −15o
	2

I tak właśnie udało mi się dojść do rozwiązania...

Trivial: o.o

Trivial: A co jeśli powiem Ci teraz, że można to zrobić tak:

	1
sin2x =
	2

	π		π
2x =		+ 2kπ lub 2x = π−		+ 2kπ
	6		6

	π		5π
x =		+ kπ lub x =		+ kπ.
	12		12

cos2x = 0

	π
2x =		+ kπ
	2

	π		π
x =		+ k*		.
	4		2

Koniec.

ICSP: nawet mnie nie wkurzaj

Trivial: I kto teraz ma rozwiązania na 3 kartki A4...

ICSP: po prostu nie wpadłem na to że sin2x można łatwiej rozwiązać. To zadanie robiłem pół roku temu. Wtedy jeszcze byłem słaby z matmy.

Trivial: Żeby rozwiązać to równanie tak jak pokazałeś to trzeba być raczej dobrym z matmy.

ICSP: Tak? Niby co tam było takiego trudnego czego by nie zrobił przeciętny uczeń klasy rozszerzonej?

Trivial: Przeciętny uczeń zgubi gdzieś minus, źle wyciągnie pierwiastek i zapomni o założeniu.

Trivial: Albo, co bardziej prawdopodobne:

	√3   −1 +   2
Zobaczy t1 =		i zrezygnuje.
	−2

ICSP: no dobrze. Z tym t₁ to może troszkę nad poziom przeciętnego ucznia, ale tylko odrobinkę.

Godzio: Można też tak: sin4x = cos2x

	π
sin4x = sin(		− 2x)
	2

	π		π
4x =		− 2x + 2kπ lub 4x =		+ 2x + 2kπ
	2		2

itd ...

ICSP: Tomek dajesz

Trivial: Cześć ISCP.

ICSP: Witaj Trivial

TOmek: wy chyba macie za dużo wiarę

TOmek: dużą*

TOmek: te zadanie trzeba zrobić głownie trygonometrią a ja znam ją średnio : |

ICSP: nie patrz na Triviala. On wszystko robi trygonometrią. Chyba nawet dodaje trygonometrią. Dałem ci podpowiedź. Musisz ułożyć drugie równanie. Obliczyć x i skorzystać z tw. cosinusów.

Trivial: Jest wiele dróg. Algebra jest fajna, bo nie trzeba myśleć nad zależnościami geometrycznymi.

ICSP: Tomku Tomku

TOmek: próbowałem wczoraj na własnej kartce zrobić to zadanie i nadal nic... ; 0

ICSP: to powiedz mi jakie drugie równanie układasz?

Trivial: Hello.

ICSP: Witamy Trivala

Basia: można też tak

	r		1
tgβ=		=
	2r		2

sinβ		1
	=
cosβ		2

cosβ=2sinβ sin²β+4sin²β=1

	1
sin2β=
	5

	4
cos2β=
	5

α= π−4β cosα= −cos4β= −2sin2βcos2β = −2*2sinβcosβ*(cos²β−sin²β) =

	1		2		2		1
−4*2*		*		*(		−		) =
	√5		√5		5		5

−16		1		−16
	*		=
5		5		25

ICSP: Niestety Basiu wynik jest inny.

Basia: A może to inne zadanie ? Bo tyle tu tego, że mogłam się pogubić.

TOmek: wybaczcie, ale znam swoje mozliwosci, to mnie przerasta, wole powoli iść do przodu

ICSP: cicho. Nic ciebie nie przerasta. Spójrz na mój rysunek i spróbuj ułożyć proporcje z podobieństwa trójkątów.

Basia: błąd jest w drugiej linijce od dołu

	1		2		4		1		−8		3		24
= −4*		*		*(		−		) =		*		= −
	√5		√5		5		5		5		5		25

Basia: oczywiście można z podobieństwa, ale to będzie znacznie więcej rachowania

Trivial:

	7
Wynik jest		.
	25

Trivial: Błąd masz w trzeciej linijce od dołu. cos2x ≠ 2sinxcosx.

Basia: no to znajdź błąd w moich obliczeniach

Basia: ach faktycznie, gdzie ja tam sinus zobaczyłam czyli policzyłam sinα (łatwiej niż cosinus), tyle, że wtedy minusa tam nie ma

	24
sinα=
	25

	576		49
cos2α = 1−		=
	625		625

	7
cosα=
	25

Basia: z wykorzystaniem podobieństwa:

h		2r		L
	=		=
L−2r		r		h−r

L
	= 2
h−r

L = 2(h−r) h²+(2r)² = L² h² +4r² = [2(h−r)²] h²+4r² = 4h² − 8hr + 4r² −3h² + 8hr = 0 −h(3h−8r) = 0 3h = 8r h = ⁸₃r L = 2(⁸₃r − r) = ¹⁰₃r

	α		2r		2r		2*3		3
sin		=		=		=		=
	2		L		103r		10		5

	α		9		16
cos2		= 1−		=
	2		25		25

	α		4
cos		=
	2		5

	α		α		16		9		7
cosα= cos2		− sin2		=		−		=
	2		2		25		25		25

mnie się bardziej podoba z wykorzystaniem tgβ