:P
ICSP: Ja na prawdę nie wiem jak to zrobić

Promień podstawy stożka jest dwa razy dłuższy od promienia kuli wpisanej w ten stożek. Oblicz
cosinus kąta rozwarcia stożka.
15 lip 10:01
Trivial:
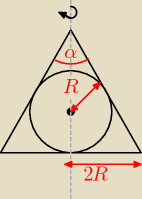
15 lip 10:13
Trivial:
Tylko co dalej.

15 lip 10:16
ICSP: zrobiłem identyczny rysunek

15 lip 10:16
ICSP: już nieważne. Udało mi się zrobić

15 lip 10:24
ICSP: ale dla Tomka będzie w sam raz

15 lip 10:25
Trivial: Już też wiem jak rozwiązać.

15 lip 10:25
ICSP: ale przyznaje na chwilę mnie to zadanie zatrzymało

15 lip 10:26
Trivial: 
15 lip 10:26
ICSP: a jaki wynik

?
15 lip 10:28
Trivial:
Myślałem że już wiem jak zrobić, ale nie.

Wyszło mi po dokończeniu cosα = cosα.

15 lip 10:32
ICSP: Brawo. To zadanie zostaw dla Tomka

Na pewno się ucieszy. Dla ciebie mam inne zadanie:
Dany jest romb o boku długości a i kącie ostrym α. Wyznacz objętość bryły otrzymanej przez
obrót tego rombu wokół dłuższej przekątnej.
Kompletnie nie wiem nawet jak to narysować

15 lip 10:35
Trivial:
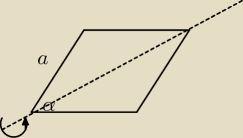
15 lip 10:39
Trivial:
Po obrocie otrzymamy "diamencik obrotowy".

15 lip 10:39
ICSP: no to teraz już może zrobię

15 lip 10:41
Trivial: Jak chcesz to mogę ci dać wskazówkę.

15 lip 10:49
ICSP: Nie trzeba.
1. Liczę obydwie przekątne
2. Połowa krótszej jest wysokością jednego z dwóch stożków o równych objętościach.
15 lip 10:56
Trivial: połowa dłuższej jest wysokością
połowa krótszej jest promieniem.

15 lip 10:59
ICSP: to bez różnicy

15 lip 11:02
Trivial: nie!

15 lip 11:03
Trivial:
btw
ISCP po co robisz te zadanka?

15 lip 11:03
ICSP: Jaka jest różnica czy za promień wezmę połowę dłuższej czy połowę krótszej?
15 lip 11:04
ICSP: sam nie wiem po co je robię

15 lip 11:04
Trivial:
Wzór na objętość stożka jest:
Chyba jednak jest różnica?

15 lip 11:04
ICSP: ale wysokość też się wtedy zmieni. Nie ma różnicy.
15 lip 11:06
ICSP: chociaż masz rację. Jest różnica:(
15 lip 11:07
Trivial:
R2
h
Zapewniam cię, jest.
15 lip 11:07
Trivial:
Będziesz miał jakieś przedmioty związane z fizyką na studiach?
15 lip 11:09
ICSP: nie wiem

Jeszcze o tym nie myślałem? Jednak liczę na to że takowych nie będzie

15 lip 11:10
Trivial:
Lepiej sprawdź, bo możesz się rozczarować (jak ja).

Wiedziałem, że fizyka będzie, ale nie przypuszczałem, że będzie taka kosmiczna.

15 lip 11:12
ICSP: nie strasz mnie
Ja z fizyki to jestem kompletna noga. Tak samo z programowania. Byłem na podstawie i w ogóle
nie wiem jak to działa:(
15 lip 11:14
Trivial:
Ja nawet nie wiedziałem jak szedłem na studia, że
F = m
a... A miałem 5 na koniec.

Jeżeli masz mieć fizykę na studiach, to lepiej to wiedzieć od razu i zacząć może się tego
uczyć już teraz, bo wymaga to zrozumienia. Jeśli chodzi o mnie, to z fizyki ledwo zdaję (czyli
| | 1 | |
i tak dobrze, bo |
| grupy nie ma tak dobrze).  Podczas wakacji mam w planie zrozumieć |
| | 3 | |
to, co było do tej pory. Jestem już prawie w połowie...
15 lip 11:19
Trivial:
Btw to nie ważne czy jesteś nogą, czy ręką z fizyki. Na studiach i tak jest start od zera. Znam
kogoś, kto miał ponad 90% z matury rozszerzonej z fizyki i... nie zdał.
15 lip 11:21
ICSP: No to teraz już się załamałem:(
15 lip 11:22
Trivial:
Czemu się załamałeś, mówię przecież, że jest start od zera (czyli fizyka licealna gra minimalną
rolę).
15 lip 11:23
ICSP: Dobra, nie ma co dramatyzować dopóki nie zobaczymy jak to będzie.
15 lip 11:25
Trivial:
A programowanie − jak to programowanie... To czy jesteś dobry zależy od tego ile ćwiczysz (tak
jak wszystko

).
Masz jeszcze jakieś zadanka?
15 lip 11:26
ICSP: Kula wpisana w stożek ma pole powierzchni dwa razy mniejsze od pola powierzchni całkowitej
stożka. Oblicz cosinus kąta nachylenia tworzącej stożka do jego podstawy.
15 lip 11:32
Trivial:
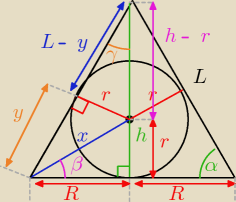
Dane:
2V
k = V
s
(0) 8r
3 = R
2h.
| | ⎧ | R2 + h2 = x2 | |
| | ⎩ | r2 + y2 = x2 |
|
y = R.
(L−y)
2 + r
2 = (h−r)
2
L
2 + R
2 − 2LR + r
2 = h
2 + r
2 − 2hr, ale L
2 = R
2 + h
2 więc
R
2 + h
2 + R
2 − 2LR = h
2 − 2hr
2R
2 − 2LR = −2hr
R
2 = LR − hr /: R
2γ + 2α = 180
o
γ = 90
o − α
hcosα − rcosα = r
hcosα = r(cosα+1)
Ale wiemy także, że
Łącząc to z równaniem (1) otrzymujemy zależność:
| | R | | R2 | | R2h | |
cosα = |
| = |
| = |
| . |
| | | | R2 + rh | | R2h + rh2 | |
Na podstawie równania (0) i (2):
Niech t = cosα.
| | 8 | | 8t2 | | 8t2 | | 9t2+2t+1 | |
t = |
| = |
| = |
| /* |
| |
| | | | 8t2+t2+2t+1 | | 9t2+2t+1 | | t | |
9t
2 + 2t + 1 = 8t
9t
2 − 6t + 1 = 0
(3t − 1)
2 = 0
3t = 1
Nie da się jakoś prościej?...
15 lip 14:01
Basia:
Trivial
2*4πr2 = πR(R+L)
tam mowa o polach powierzchni, i to się dopiero komplikuje
15 lip 14:08
Trivial: O pola powierzchni... no tak.

15 lip 14:09
Basia: Koszmary mi wychodzą i chyba jednak pojadę nad jakąś wodę. Może wieczorem pomyślę, bo mój umysł
dopiero koło 20:00 zaczyna działać na pełnych obrotach.
15 lip 14:12
ICSP: Wynik dobry

15 lip 14:17
Trivial:
| | 1 | |
cosα = |
| jeśli chodzi o pola powierzchni  |
| | 7 | |
15 lip 14:21
Trivial:
ISCP jaki tam wynik podają?
15 lip 14:22
15 lip 14:33
Trivial:
| | 1 | |
Wyszło mi |
| dla pól teraz. |
| | 3 | |
15 lip 14:58
Basia:
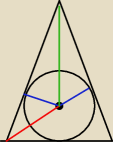 Trivial
Trivial a skąd Ci się wzięło, że odcinek czerwony = zielony ?
Tak wcale być nie musi
15 lip 15:59
Trivial: A gdzie tak napisałem?
15 lip 16:08
Basia: poza tym gdyby y=R ⇒ L=2R ⇒ α=60
15 lip 16:08
Basia:
tak jest na Twoim rysunku; zakładasz, że punkt styczności dzieli L na dwa równe odcinki
tak być nie musi (i co więcej w tym przypadku na pewno nie jest)
chyba, że jakoś źle ten rysunek czytam
15 lip 16:10
Trivial:
Zaraz pod równaniem (0) mamy:
R
2 + h
2 = x
2
Powinno być:
R
2 + r
2 = x
2
Literówka.

15 lip 16:13
Trivial: Rysunek niestety nie mógł być dużo bardziej czytelny, bo zadanie jest dosyć skomplikowane.
15 lip 16:14
Basia:
źle czytam; już widzę czego nie widziałam [P[L] mi gdzieś zginęło
15 lip 16:14
Trivial:
To rozwiązanie jest dla objętości, ale wersja dla pól nie wymaga dużej ilości poprawek.
Wynik wychodzi taki sam, co jest dosyć podejrzane. ;>
15 lip 16:16
Basia:
a i jeszcze za diabła nie rozumiem, skąd Ci się wzięło
R2+h2 = x2 ?
15 lip 16:19
Trivial:
Dla pól trzeba zmienić równanie (0) na:
8r
2 = R
2 + LR
a następnie skorzystać z (1), (2) i faktu, że:
15 lip 16:20
Trivial: Literówka, napisałem wyżej jak powinno być.
15 lip 16:21
Basia:
tak, ale skąd masz R2+h2 = x2 (przecież to nieprawda, może literówka ?)
15 lip 16:22
Trivial:
Zaraz pod równaniem (0) mamy:
R2 + h2 = x2
Powinno być:
R2 + r2 = x2
Literówka.
15 lip 16:24
Basia:
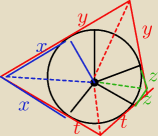
to, że y=R wiemy natychmiast z przystawania trójkątów
nie musisz tego w ten sposób dowodzić
tak jest nie tylko w trójkącie, ale w każdym wielokącie opisanym na okręgu
15 lip 16:41
Basia: poza tym wszystko mi się wydaje w porządku; spróbuję jeszcze raz przeliczyć na wszelki wypadek,
ale tak jak czytam żadnego błędu nie widzą
15 lip 16:43
 Promień podstawy stożka jest dwa razy dłuższy od promienia kuli wpisanej w ten stożek. Oblicz
cosinus kąta rozwarcia stożka.
Promień podstawy stożka jest dwa razy dłuższy od promienia kuli wpisanej w ten stożek. Oblicz
cosinus kąta rozwarcia stożka.








 ?
?
 Wyszło mi po dokończeniu cosα = cosα.
Wyszło mi po dokończeniu cosα = cosα. 
 Na pewno się ucieszy. Dla ciebie mam inne zadanie:
Dany jest romb o boku długości a i kącie ostrym α. Wyznacz objętość bryły otrzymanej przez
obrót tego rombu wokół dłuższej przekątnej.
Kompletnie nie wiem nawet jak to narysować
Na pewno się ucieszy. Dla ciebie mam inne zadanie:
Dany jest romb o boku długości a i kącie ostrym α. Wyznacz objętość bryły otrzymanej przez
obrót tego rombu wokół dłuższej przekątnej.
Kompletnie nie wiem nawet jak to narysować










 Jeszcze o tym nie myślałem? Jednak liczę na to że takowych nie będzie
Jeszcze o tym nie myślałem? Jednak liczę na to że takowych nie będzie
 Wiedziałem, że fizyka będzie, ale nie przypuszczałem, że będzie taka kosmiczna.
Wiedziałem, że fizyka będzie, ale nie przypuszczałem, że będzie taka kosmiczna. 
 Jeżeli masz mieć fizykę na studiach, to lepiej to wiedzieć od razu i zacząć może się tego
uczyć już teraz, bo wymaga to zrozumienia. Jeśli chodzi o mnie, to z fizyki ledwo zdaję (czyli
Jeżeli masz mieć fizykę na studiach, to lepiej to wiedzieć od razu i zacząć może się tego
uczyć już teraz, bo wymaga to zrozumienia. Jeśli chodzi o mnie, to z fizyki ledwo zdaję (czyli
 Podczas wakacji mam w planie zrozumieć
Podczas wakacji mam w planie zrozumieć ).
Masz jeszcze jakieś zadanka?
).
Masz jeszcze jakieś zadanka?
 Dane:
2Vk = Vs
Dane:
2Vk = Vs



 Trivial a skąd Ci się wzięło, że odcinek czerwony = zielony ?
Tak wcale być nie musi
Trivial a skąd Ci się wzięło, że odcinek czerwony = zielony ?
Tak wcale być nie musi

 to, że y=R wiemy natychmiast z przystawania trójkątów
nie musisz tego w ten sposób dowodzić
tak jest nie tylko w trójkącie, ale w każdym wielokącie opisanym na okręgu
to, że y=R wiemy natychmiast z przystawania trójkątów
nie musisz tego w ten sposób dowodzić
tak jest nie tylko w trójkącie, ale w każdym wielokącie opisanym na okręgu