 1.
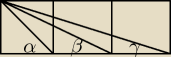
Trzy kwadraty mają jednakowy rozmiar i są przystające(rys.) Znajdz sumę kątów α+β+γ
2.
W ostrosłup trójkątny o wysokościach h1, h2, h3 ,h4 wpisano kulę o promieniu r.Udowodnić
,że r−1=h1−1+h2−1+h3−1+h4−1
3.
1.
Trzy kwadraty mają jednakowy rozmiar i są przystające(rys.) Znajdz sumę kątów α+β+γ
2.
W ostrosłup trójkątny o wysokościach h1, h2, h3 ,h4 wpisano kulę o promieniu r.Udowodnić
,że r−1=h1−1+h2−1+h3−1+h4−1
3.
| π | ||
Wiadomo że a>0, 0<α< | ||
| 2 |
| 1 | ||
Udowodnić , że (a+U{1}{cosα)(a+ | > a2+2a+2
| |
| sinα |
| 1 | 1 | |||
Udowodnij że (a+ | )(a+ | ) > a2+2a+2
| ||
| cosα | sinα |
| π | ||
a>0 0<α< | ||
| 2 |
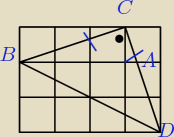 1) Rysujemy trójkąt BDC jak wyżej, z tw. odwrotnego do tw. Pitagorasa pokazujemy, że jest on
prostokątny, z tw. Pitagorasa pokazujemy, że jest on równoramienny, czyli kąt DBC = 45*, ale
nietrudno zauważyć, że w naszym zadaniu β = kąt DBA oraz γ = kąt ABC czyli
β+γ = DBA+ABC = 45*, dodajemy do tego kąt α = 45* (wiadomo czemu 45*) i otrzymujemy:
α+β+γ = 90*
1) Rysujemy trójkąt BDC jak wyżej, z tw. odwrotnego do tw. Pitagorasa pokazujemy, że jest on
prostokątny, z tw. Pitagorasa pokazujemy, że jest on równoramienny, czyli kąt DBC = 45*, ale
nietrudno zauważyć, że w naszym zadaniu β = kąt DBA oraz γ = kąt ABC czyli
β+γ = DBA+ABC = 45*, dodajemy do tego kąt α = 45* (wiadomo czemu 45*) i otrzymujemy:
α+β+γ = 90*
| 1 | 190 | |||
−63a3 = −1 ⇔ a3 = | ⇒ x = a3+3 = | |||
| 63 | 63 |
| 1 | 2185 | |||
W 2 przypadku otrzymujemy −728a3=−1 ⇔ a3 = | ⇒ x = | czyli dane równanie | ||
| 728 | 728 |
| 190 | 2185 | |||
ma 2 rozwiązania x = | v x = | |||
| 63 | 728 |
 a co z zadaniami 2,3 i 6 ?
a co z zadaniami 2,3 i 6 ?
| 1 | 1 | 1 | 1 | 1 | ||||||
2) Mamy pokazać | = | + | + | + | , ze wzoru na objętość | |||||
| r | h1 | h2 | h3 | h4 |
| P1*h1 | 1 | P1 | ||||
V = | ⇔ 3V = P1*h1 ⇔ | = | ||||
| 3 | h1 | 3V |
| 1 | P2 | 1 | P3 | 1 | P4 | ||||||
= | , | = | , | = | sumując dostajemy: | ||||||
| h2 | 3V | h3 | 3V | h4 | 3V |
| 1 | 1 | 1 | 1 | 1 | |||||
+ | + | + | = | (P1+P2+P3+P4) | |||||
| h1 | h2 | h3 | h4 | 3V |
| 3V | |
= P1+P2+P3+P4 | |
| r |
| P1*r | ||
V1 = | ||
| 3 |
| r | ||
V = V1+V2+V3+V4 = | (P1+P2+P3+P4) ⇔ 3V = r(P1+P2+P3+P4) teraz wystarczy | |
| 3 |
| 1 | 1 | 1 | ||||
a2 + a( | + | )+ | > a2+2a+2 | |||
| sinα | cosα | sinαcosα |
| 1 | 1 | 1 | ||||
a( | + | ) + | > 2a+2 | |||
| sinα | cosα | sinαcosα |
| 1 | |
≥ 2 ⇔ 1 ≥ 2sinαcosα = sin(2α) co jest oczywiste, czyli mamy dowieść, że: | |
| sinαcosα |
| 1 | 1 | ||
+ | > 2 ⇔ sinα+cosα > 2sinαcosα ⇔ sinα(1−cosα)+cosα(1−sinα) > 0 co będzie | ||
| sinα | cosα |