PROblem TOmek: Przez punkt A=(2, 3) poprowadzono prostą odcinającą na półosiach układ współrzędnych odcinki równej długości. znajdż równanie tej prostej −−−−−−−−−−−−−−−−−−− niby łatwe zadanie a wynik nie chce wyjśc

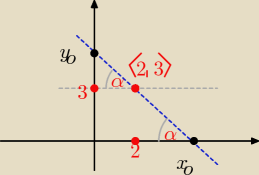
Jack: y₀=x₀

	y0−3		y0
Stąd tgα=		=		=1 ⇒ y0=x0=5
	2		x0

Potem tylko do układu równań i mamy prostą.

TOmek: w odpowiedziach mam dwie proste y=x+1 i y=−x+5 3=2x+b 0=5x+b b=3−2x 0=5x+3−2x 0=3x+3 x=−1 hmmm? a druga prosta?

TOmek: juz, wiem ,trudny sposob wybrałes, dziekuje

Jack: widziałem kiedyś podobne zadanie i chodziło o dodatnie półosie... Tutaj faktycznie tak nie jest. Można oczywiście inaczej przeprowadzić tę prostą... Znalazłeś inną metodę do tego zadania?

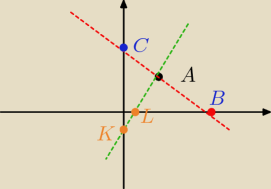
TOmek: C=(0,p) B=(p,0) 3=2a+b p=b 0=pa+b −−−−−−−−−−−−−− K=(0,−c) L=(c,0) 3=2a+b −c=b 0=ca+b nie wiem czy z tego wyjdzie dobry wynik, bo jestem zbyt zmęczony by sprawdzić, rzuć tylko okiem czy na "oko" jest dobrze? tak myślałem o 3 prostej, jednak na "oko" mozna zauwazyc ,ze to niemozliwe

Jack: tak, zdaje się że tak można − podobnie pomyślałem. Ale mi chodziło o "zasadniczo" inną metodę rozwiązania tego zadania To co napisałeś, to włąścwie to samo co wykorzystaliśmy wcześniej. Mam na myśli sposób bazujący na długości odcinków itp

TOmek: to gitara, jutro jeszcze oblicze to wszystko i sprawdze czy rzeczywiscie sie zgadza, Dziekuje pięknie za dzisiejszą pomoc Jack, Dobranoc

Jack: bardzo proszę, dobranoc!

Jack: PS Trzeba jeszcze sprawdzić dla porządku przypadek: A(−c,0) i B(0,c)

rumpe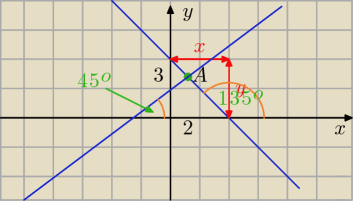k: Jack może być taka? (rysunek oczywiście "teoretyczny" ) 1^o z polecenia wynika, że moje oznaczone na rysunku x i y są sobie równe więc x = y, czyli jest to trójkąt prostokątny o kątach 90^o, 45^o, 45^o. Widać na rysunku, że jest to funkcja malejąca więc wzór będzie miała: y = −ax + b. Wiemy jednak o kątach mianowicie: 180^o − 45^o = 135^o. A tg135^o = −1 Czyli mamy przypadek gdy: a = −1 (pozostaje rozwiązać układ równań) y = −x + b 3 = −2 + b ⇒ b = 5 Trzeba jeszcze rozpatrzyć drugą sytuacje − kiedy funkcja liniowa jest rosnąca i jej współczynnik a jest dodatni, czyli a. Znowu korzystamy z "kąta nachylenia prostej do osi x". I mamy: tg45^o = 1 I dla a = 1 mamy: y = x + b 3 = 2 + b ⇒ b = 1 Czyli równania prostych to: y = −x + 5 oraz y = x + 1

Jack: fajnie , no i teoretycznie trzeba sprawdzić trzecią opcję.

rumpek: "Mam na myśli sposób bazujący na długości odcinków itp " Chyba masz to na myśli (już bez rysunków bo to nudne jest )

	x		y
Korzystając z "http://www.math.edu.pl/rownanie-odcinkowe-prostej" mamy tam:		+		= 1
	a		b

Na powyższym rysunku i w "opisie" pod rysunkiem napisałem, że x = y (w tej sytuacji zostanie to oznaczone jako a i b, czyli a = b [zatem mogę podstawić za b, a])

x		y
	+		= 1
a		a

x + y
	= 1
a

Podstawiając to pod ten punkt A(2,3) mam:

2 + 3
	= 1 / * a ⇒ a = 5, więc ostatecznie mam:
a

x + y
	= 1
a

x + y
	= 1 / * 5
5

x + y = 5 y = −x + 5 To dla a = −1 (funkcja malejąca jeszcze druga została) To robię teraz dla: −a i a

x		y
	+		= 1
−a		a

Znowu podstawiam A(2,3) i mam:

	2		3
−		+		= 1 / * a
	a		a

−2 + 3 = a ⇒ a = 1 I ponownie:

	x		y
−		+		= 1
	1		1

−x + y = 1 y = x + 1 Czyli proste to: y = −x + 5 oraz y = x + 1

Jack: nieźle próbujesz Miałem na myśli coś takiego jako punkt wyjścia: |y₀−0|=|x₀−0| ⇒ |y₀|=|x₀| I teraz 3 możliwości: y₀>0 i x₀>0 lub .... itp. Odpada opcja y₀<0 i x₀<0 ponieważ punkt A na pewno nie należałby do takiej prostej. No i teraz trzeba by po kolei wyznaczać możliwe proste.

Basia: y = ax+b 3 = a*2+b 2a+b=3 b = 3−2a prosta przecina oś OY w p−cie (0,b) a oś OX w p−cie (−^b_a,0) czyli długość odcinka na OY to |b|, a długość odcinka na OX to |−^b_a|=|^b_a| stąd: |b| = |^−b_a| |b| = |^b_a| ⇔ |a|=1 ⇔ a=1 lub a= −1 a=1 ⇒ b =3−2=1 i masz prostą y=x+1 a=−1 ⇒ b = 3+2=5 i masz prostą y= −x+5 chyba nieco mniej liczenia

QWERTY: wybaczcie za odk opanie ale mam pytanie dlaczego OX jest (−b\a,0) skad to −b\a?

aniabb: y=ax+b z OX y=0 0=ax+b ax=−b x=−b/a

PW:

	3
A ja myślę, że prosta y=		x też spełnia warunki zadania − odcina na półosiach odcinki o
	2

z e r o w e j długości − też są równe.