Oblicz pole obszaru ograniczonego wykresami funkcji Reynevan: Oblicz pole obszaru ograniczonego wykresami funkcji

	x
f(x)=arctgx g(x)=arcctgx y=
	2

Szczerze powiedziawszy nie mam pojęcia jak rozwiązać zadania zawierające trzy funkcje. Wiem, że gdy były dwie podstawiało się do całki, ale nie wiem co mam zrobić teraz. Pomożecie rozwiązać ?

Basia: trzeba poszukać punktów wspólnych, naszkicować wykresy i ustalić granice całkowania arctgx = arcctgx tgx = ctgx

	π
x =
	4

to proste, ale dalej zaczynają się schody, bo nie wiem jak rozwiązać równania arctgx = ^x₂ (to ma dwa rozwiązania x=0 i jak znaleźć drugie ?) i arcctgx = ^x₂ (to ma jedno rozwiązanie) spróbuję to mniej więcej naszkicować

Basia:

	π
x0 =
	4

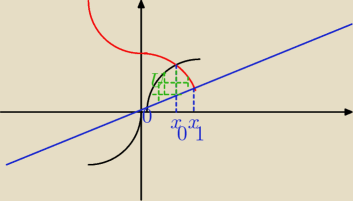
P = ₀∫^x₀ [ arctgx − ^x₂] + _x0∫^x₁ [ arcctgx − ^x₂ ] problemem jest wyznaczenie x₁, bo drugi punkt przecięcia f(x) = arctgx z prostą już nas nie obchodzi czyli trzeba rozwiązać równanie

	x
arcctgx =
	2

nie mam pomysłu

Reynevan: http://www.wolframalpha.com/input/?i=arcctgn%28x%29%3Dx%2F2 Wolfram powiada, że x to około 1,3 Myślisz, że mogę sobie podstawić 1,3 ?

Basia: nie mam pojęcia, to co podaje Wolfram to tylko przybliżenie, a tu chyba powinna być dokładna wartość

Reynevan: Teraz dopiero zauważyłem, czy przypadkiem ta czerwona linia to nie jest wykres arccos ? Arcctg wygląda inaczej jeśli dobrze pamiętam

Basia: one mi strasznie pokraczne wyszły; powinny się ciągnąć do nieskończoności

	π		π
arctgx jest ograniczony asymptotami y = −		i y =		, rośnie i oś OY przecina w 0
	2		2

	π
arcctgx jest ograniczony asymptotami y=0 i y=π, maleje i oś OY przecina w
	2

Reynevan: Hmm nikt nie ma pomysłu jak to dalej zrobić ?

AS: Przybliżony szukany punkt to: 2.3311

Basia: oczywiście bzdurę kompletną tam napisałam x₀ = 1 arctgx = arcctgx = y ⇔ tgy = ctgy = x ⇔

	π
y =		⇔ x=1
	4

ale równania

	x
arcctgx =		nadal nie potrafię rozwiązać
	2

AS: Basiu! Pozostają metody przybliżone np. średnich arytmetycznych,reguła falsi.

Basia: strasznie ich nie lubię, a poza tym te metody na egzamin ? no chyba, że to było w ramach ćwiczeń, albo założymy, że można korzystać w takich wypadkach np. z Wolframy (bo niby dlaczego nie ?)